三分经典例题与真题集合-程序员宅基地
文章目录
三分用以解决单峰函数求峰值问题。
实数三分
实数三分模板:
double l = L, r = R;
while(r - l > 1e-7)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) < check(rmid)) l = lmid; //如果是中间凸的单峰函数是<号,中间凹是>号。
else r = rmid;
}
printf("%.10f", l); //l为最佳位置,check(l)为峰值。
例1,模板题
Link
给出一个 N N N 次函数,保证在范围 [ l , r ] [l, r] [l,r] 内存在一点 x x x,使得 [ l , x ] [l, x] [l,x] 上单调增, [ x , r ] [x, r] [x,r] 上单调减。试求出 x x x 的值。
思路
实数三分的模板题,每次将当前区间分成三段 [l, l+(r-l)/3], [l+(r-l)/3, r-(r-l)/3], [r-(r-l)/3, r],根据分界点 l+(r-l)/3 和 r-(r-l)/3 时结果的大小,舍弃掉答案不在的那段,剩余两段。
所以三分到答案最近的整数的复杂度为 O ( 2 l o g 3 n ) O(2log_3n) O(2log3n),近似于 O ( 2 l o g n ) O(2logn) O(2logn)。如果再精确范围到几位小数的话,复杂度相应增大。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
double a[N];
double L, R;
double check(double x){
double sum = 0;
for(int i=0;i<=n;i++)
{
double t = 1;
for(int j=1;j<=i;j++) t *= x;
sum += a[i] * t;
}
return sum;
}
signed main(){
Ios;
cin >> n;
cin >> L >> R;
for(int i=n;i>=0;i--) cin >> a[i];
double l = L, r = R;
while(r - l > 1e-7)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) < check(rmid)) l = lmid;
else r = rmid;
}
printf("%.10f", l);
return 0;
}
例2,Party All the Time
Link
给定一维坐标系中的 n 个人,每人有位置 x i x_i xi 和 重量 w i w_i wi。
如果所在位置为 x i x_i xi 的人走到位置 P P P 的话,花费为 ∣ P − x i ∣ 3 ∗ w i |P-x_i|^3*w_i ∣P−xi∣3∗wi。
选定一个位置,使得所有人到这个位置的花费之和最小,输出最小和。
1 < = N < = 5 ∗ 1 0 4 , ∣ x i ∣ < = 1 0 6 , 0 < w i < 15 1<=N<=5*10^4,\ |x_i |<=10^6 , 0<w_i <15 1<=N<=5∗104, ∣xi∣<=106,0<wi<15
思路
直观上感觉,如果P位置太靠左的话,右边的点过来就要耗费更多花费,如果太靠右的话,左边的点过来就要耗费更多花费。最佳方案就是把 P 放到中间。
也就是说,总花费是一个中间凹的单峰函数。
所以可以三分位置,找到最佳位置。
Code
//http://acm.hdu.edu.cn/showproblem.php?pid=4355
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
double pos, w;
}a[N];
double check(double x)
{
double sum = 0;
for(int i=1;i<=n;i++)
{
double s = fabs(a[i].pos - x);
sum += s * s * s * a[i].w;
}
return sum;
}
signed main(){
scanf("%lld", &T);
for(int cs = 1; cs <= T; cs ++)
{
scanf("%lld", &n);
for(int i=1;i<=n;i++)
{
double x, w; scanf("%lf%lf", &x, &w);
a[i] = {
x, w};
}
double l = -1e6, r = 1e6;
for(int i=1;i<=100;i++)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid;
else r = rmid;
}
printf("Case #%lld: %.0f\n", cs, check(l));
}
return 0;
}
变式:P1883 函数
整数三分
就只需要将答案三分到最接近峰值的整数即可,但模板有些不同。
int l = 0, r = 1e9;
while(l < r)
{
int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) < check(rmid)) l = lmid + 1; 如果是中间凸的单峰函数是<号,中间凹是>号。
else r = rmid - 1;
}
cout << check(l) << endl; //l为最佳位置,check(l)为峰值。
例1,E. Restorer Distance (+贪心)
Link
给定长度为 n 的整数数列,可以进行若干次下面操作:
- 将某个位置上的值 + 1,花费为 A A A;
- 将某个位置上的值 - 1,花费为 R R R;
- 选择两个位置 i , j i,j i,j,将 a [ i ] − 1 , a [ j ] + 1 a[i]-1,\ a[j]+1 a[i]−1, a[j]+1,花费为 M M M。
问,使得所有数相同的最小花费为多少?
思路
如果将所有数都变得很小的话,那么原来很大的值要花费很多才能变过来;如果将所有数都变得很大的话,原来很小的值也要花费很多才能变过来。所以最佳方案就是把所有数变到中间的一个值。
花费之和 对于 最后变成的值 形成了一个中间凹的单峰函数。
三分最后变成的值,得到最小花费。
因为原来是整数,每次变化都使其+1或-1,所以最终变成的值也是整数,三分只考虑整数。
check 的时候贪心考虑,如果 M > A+R 的话就先用操作三,否则就只用操作一和二。
Code
//https://codeforces.com/problemset/problem/1355/E
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
int cost1, cost2, cost3;
int check(int mid)
{
int sum1 = 0, sum2 = 0;
for(int i=1;i<=n;i++){
if(a[i] > mid) sum1 += a[i] - mid;
else sum2 += mid - a[i];
}
int ans = 0;
if(cost3 < cost1 + cost2)
{
if(sum1 >= sum2){
ans += sum2 * cost3;
sum1 -= sum2;
ans += sum1 * cost2;
}
else
{
ans += sum1 * cost3;
sum2 -= sum1;
ans += sum2 * cost1;
}
}
else
{
ans += sum1 * cost2 + sum2 * cost1;
}
return ans;
}
signed main(){
Ios;
cin >> n >> cost1 >> cost2 >> cost3;
for(int i=1;i<=n;i++) cin >> a[i];
int l = 0, r = 1e9;
while(l < r)
{
int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid + 1;
else r = rmid - 1;
}
cout << check(l) << endl;
return 0;
}
例2,P3745 [六省联考 2017] 期末考试 (+贪心)
Link
有 n n n 位同学参加了全部的 m m m 门课程的期末考试,等待成绩的公布。
第 i i i 位同学希望在第 t i t_i ti 天或之前得知所有课程的成绩。如果在第 t i t_i ti 天,有至少一门课程的成绩没有公布,他就会等待最后公布成绩的课程公布成绩,每等待一天就会产生 C C C 不愉快度。
对于第 i i i 门课程,按照原本的计划,会在第 b i b_i bi 天公布成绩。
有如下两种操作可以调整公布成绩的时间:
- 公布课程 X X X 成绩的时间推迟一天,公布课程 Y Y Y 成绩的时间提前一天;每次操作产生 A A A 不愉快度。
- 学科 Z Z Z 的出成绩时间提前一天;每次操作产生 B B B 不愉快度。
通过若干次操作,使得总的不愉快度之和最小,输出最小的不愉快度之和。
1 ≤ n , m , t i , b i ≤ 1 0 5 , 0 ≤ A , B , C ≤ 1 0 5 1 \leq n, m, t_{i}, b_{i} \leq 10^{5},\ 0 \leq A, B, C \leq 10^{5} 1≤n,m,ti,bi≤105, 0≤A,B,C≤105
思路
如果最后一门课程公布的时间太晚的话,那么 n 位同学等待时间就很大;如果最后一门课程公布的时间太早的话,需要花费更多来调度。所以总的花费对最后一门课程公布的时间呈中间凹的单峰函数。可以通过三分最后一门课程公布的时间来找到最小花费。
check时贪心操作,对于当前最后一门公布的时间已知,那么所有同学等待的时间便是固定的,关键在于如何调度使得花费最小。如果说,交换的花费比减小的花费少的话,就尽可能交换,实在不行再减小。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll __int128
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N], b[N];
int A, B, C;
ll check(int ddl)
{
ll sum = 0;
for(int i=1;i<=n;i++){
if(ddl > a[i]) sum += C*(ddl - a[i]);
}
if(B < A)
{
for(int i=1;i<=m;i++)
if(b[i] > ddl) sum += B*(b[i] - ddl);
}
else
{
ll s = 0;
for(int i=1;i<=m;i++)
if(b[i] < ddl) s += ddl - b[i];
for(int i=1;i<=m;i++)
{
if(b[i] > ddl)
{
int x = b[i] - ddl;
if(s > x) s -= x, sum += A*x;
else{
sum += A*s;
x -= s;
s = 0;
sum += B*x;
}
}
}
}
return sum;
}
void print(ll x)
{
if(x > 9) print(x / 10);
putchar('0' + x%10);
}
signed main(){
Ios;
cin >> A >> B >> C;
cin >> n >> m;
for(int i=1;i<=n;i++) cin >> a[i];
for(int i=1;i<=m;i++) cin >> b[i];
int l = 1, r = 1e5;
while(l < r)
{
int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid + 1;
else r = rmid - 1;
}
print(check(l));
return 0;
}
其实,这题可以用前缀和提前预处理出每个截止日期的花费,然后O(1)判断。所以可以直接枚举或者用三分再优化。
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int unsigned long long
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N], b[N];
int cnt1[N], cnt2[N];
int A, B, C;
int suma[N], sumb[N];
signed main(){
Ios;
cin >> A >> B >> C;
cin >> n >> m;
for(int i=1;i<=n;i++) cin >> a[i];
sort(a+1, a+n+1);
for(int i=1;i<=n;i++) suma[i] = suma[i-1] + a[i];
for(int i=1;i<=m;i++) cin >> b[i];
sort(b+1, b+m+1);
for(int i=1;i<=m;i++) sumb[i] = sumb[i-1] + b[i];
int mina = 1e18;
int idx1 = 0, idx2 = 0;
for(int i=1;i<=b[m];i++)
{
while(idx1 + 1 <= n && a[idx1 + 1] <= i) idx1 ++;
while(idx2 + 1 <= m && b[idx2 + 1] <= i) idx2 ++;
int ans = C * (idx1 * i - suma[idx1]);
int left = 0, need = 0;
left = idx2 * i - sumb[idx2];
need = sumb[m] - sumb[idx2] - (m-idx2)*i;
if(A<B)
{
if(left > need) ans += need*A;
else{
ans += left*A;
need -= left;
ans += need*B;
}
}
else ans += need * B;
mina = min(mina, ans);
}
cout << mina << endl;
return 0;
}
例3,P4040 [AHOI2014/JSOI2014] 宅男计划 (+贪心)
Link
一共 n 种食物,每种食物有价格 p i p_i pi 和 保质期 s i s_i si。
第 i 种食物将在买来之后的第 s i s_i si 天过期,比如今天买了一份保质期为 1 天的食物,那么必须在今天或者明天吃掉,保质期为 0 天必须在购买当天吃掉。
现在有 m m m 块钱。每次点外卖需要付运费 f f f 元,可以带来任意多份食物。
问,在满足每天至少吃一顿的情况下,最多可以点多少天?
1 ≤ n ≤ 200 , 0 ≤ s i ≤ 1 0 18 , 1 ≤ f , p i , m ≤ 1 0 18 1 \leq n \leq 200,0 \leq s_{i} \leq 10^{18}, 1 \leq f, p_{i}, m \leq 10^{18} 1≤n≤200,0≤si≤1018,1≤f,pi,m≤1018
思路
当点外卖的次数较少时,其可能要选择保质期长但较贵的食物,购买的食物数量减少;当点外卖的次数较多时,其需要多付运费,导致其购买的食物数量减少。所以只有当点外卖的次数到某个中间值的时候,其买的食物最多。购买的食物呈中间凸的单峰函数。
所以可以三分点外卖的次数,求出购买食物的最大数量。
check函数中,当点外卖的次数固定下来时,需要贪心的考虑每次点哪些外卖。
对于 k 次订购,每次肯定都按最佳策略订,所以前面点的种类和个数都是相同的,只有最后某种不能买 k 次了,有一些次订购多了这种。
把所有外卖按照价格从小到大排序,价格相同时保质期较长的放在前面,每次判断当前种类当 k 次订购都点时最多能点几份,同时还有保质期限制。
如果发现当前钱数对于 k 次订购一份都点不了时,说明后面都点不了了,退出。
只能订购某种外卖若干次以便将所有钱花完,到不了 k 次了。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll unsigned long long
const int N = 200010, mod = 1e9+7;
int T, n, m;
int f;
PII a[N];
bool cmp(PII a, PII b){
if(a.fi != b.fi) return a.fi < b.fi;
return a.se > b.se;
}
int check(ll k)
{
if(k*f >= m || k == 0) return 0;
ll w = m - k*f;
ll ans = 0;
//每次订购时都买这种,每次尽可能买多份,以使得花费最少,买的最多
int now = 0;
for(int i=1;i<=n;i++)
{
if(a[i].se >= now)
{
if(w < k*a[i].fi) break; //如果当前价格一份也不能买,那么后面都不能买,退出
else
{
ll fen = min(w/(k*a[i].fi), (ll)a[i].se - now + 1); //每次订购时能买的份数,钱数或者保质期限制
w -= fen * k * a[i].fi;
now += fen;
ans += k * fen;
}
}
}
//剩下的钱虽然不能每次订购都买一份了,但是可能在某些次订购的时候多买一份,求出多买的份数
for(int i=1;i<=n;i++)
{
if(a[i].se >= now)
{
ll fen = w/a[i].fi;
// w -= fen * a[i].fi;
// now += fen;
ans += fen;
break;
}
}
return ans;
}
signed main(){
Ios;
cin >> m >> f >> n;
for(int i=1;i<=n;i++) cin >> a[i].fi >> a[i].se;
sort(a+1, a+n+1, cmp);
int l = 0, r = m/f;
while(l < r)
{
int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) < check(rmid)) l = lmid + 1;
else r = rmid - 1;
}
cout << check(l);
return 0;
}
计算几何中的三分
例1,4180. 灯泡
Link
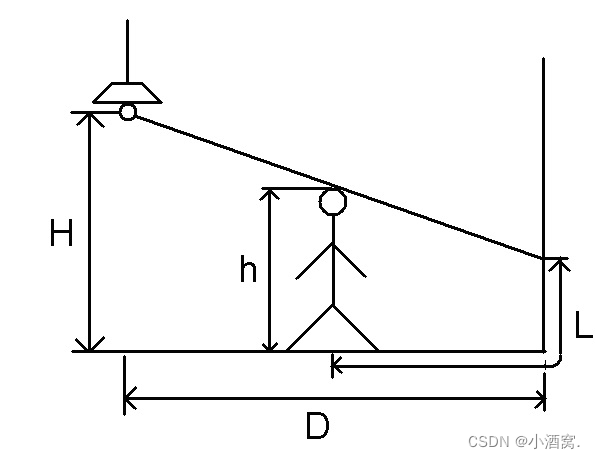
给定 H , h , D H,\ h,\ D H, h, D,人在 D 上移动,左上角为灯泡。
求影子 L L L 的最长长度。
思路
当人太靠左时,影子可能不会投射到右面的墙上,影子的长度很短;当人太靠右时,影子会过多投射到墙上,最长长度为人的身高。而在中间某个位置时,影子在地面上拉长并可能有一部分投射到墙上,总长度最长。
所以影子的长度随着人的位置呈中间凸的单峰函数,三分人的位置求峰值。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
double H, h, D;
int bi(double x, double y){
//减少精度误差
if(fabs(x - y) < 1e-6) return 0;
if(x > y) return 1;
return -1;
}
double check(double x)
{
if(bi(x, 0) == 0) return 0;
if(bi(x + x*h/(H-h), D) <= 0) return x*h/(H-h); //影子未投射到墙上
double ans = H - D*(H-h)/x;
return D - x + ans;
}
signed main(){
Ios;
cin >> T;
while(T--)
{
cin >> H >> h >> D;
double l = 0, r = D;
for(int i=1;i<=1000;i++)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) < check(rmid)) l = lmid;
else r = rmid;
}
printf("%.3f\n", check(l));
}
return 0;
}
例2,Stealing a Cake
Link
在二维坐标上,有点 S ( x , y ) S\ (x, y) S (x,y)、圆心为 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)、半径为 r r r 的圆、一个相对顶点为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),\ (x_2,y_2) (x1,y1), (x2,y2) 边与坐标轴平行的矩形。
保证三种图形互不重叠。
问,从起点出发,触及圆周任一点后,再触及矩形的最小路径长度为多少?
1 0 4 ≤ x t , y t ≤ 1 0 4 10^4≤x_t,y_t≤10^4 104≤xt,yt≤104
思路
以任意位置为分界线将圆分为两个半圆,点 S 到圆上一点再到矩形的距离一定满足,在一个半圆上先增后减,在另一个半圆上先减后增。
按照圆心角 [ 0 , π ] [0, π] [0,π] 和 [ π , 2 π ] [π, 2π] [π,2π] 分成两个半圆,对于每个半圆,三分其圆心角,求峰值(最小值)。
圆心角 du 固定了,那么圆上的点为 x = x0 + r * cos(du), y = y0 + r * sin(du),到矩形的最小距离为:到矩形四个边距离的最小值。
Code
//http://acm.hdu.edu.cn/showproblem.php?pid=4454
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
const double PI = acos(-1);
int T, n, m;
struct node{
double x, y;
};
double r;
node st, c, a[N];
int bi(double x, double y){
if(fabs(x - y) <= 1e-6) return 0;
if(x > y) return 1;
return -1;
}
double dis(node a, node b){
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double distoline(node p, node a, node b)
{
double ap = (b.x-a.x)*(p.x-a.x)+(b.y-a.y)*(p.y-a.y);
if(bi(ap, 0) <= 0) return sqrt((p.x-a.x)*(p.x-a.x)+(p.y-a.y)*(p.y-a.y));//最短为ap
double ab = (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
if(bi(ap, ab) >= 0) return sqrt((p.x-b.x)*(p.x-b.x)+(p.y-b.y)*(p.y-b.y));//最短为bp
double r = ap/ab;
double px = a.x+(b.x-a.x)*r;
double py = a.y+(b.y-a.y)*r;
return sqrt((p.x-px)*(p.x-px)+(p.y-py)*(p.y-py));//垂线距离
}
double check(double du)
{
double x = c.x + r * cos(du), y = c.y + r * sin(du);
node pos = {
x, y};
double mina = 1e18;
for(int i=1;i<=4;i++)
mina = min(mina, distoline(pos, a[i], a[i%4 + 1]));
return mina + dis(pos, st);
}
double pd(double l, double r)
{
for(int i=1;i<=100;i++)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid;
else r = rmid;
}
return check(l);
}
signed main(){
Ios;
while(cin >> st.x >> st.y && !(bi(st.x, 0) == 0 && bi(st.y, 0) == 0))
{
cin >> c.x >> c.y;
cin >> r;
cin >> a[1].x >> a[1].y >> a[3].x >> a[3].y;
if(bi(a[1].y, a[3].y) < 0) swap(a[1], a[3]);
a[2] = {
a[3].x, a[1].y};
a[4] = {
a[1].x, a[3].y};
double ans = 1e18;
ans = min(ans, pd(0, PI));
ans = min(ans, pd(PI, 2*PI));
printf("%.2lf\n", ans);
}
return 0;
}
三分套三分
如果在两个变量都未知的情况下,整体是可以三分的,然后当一个变量确定的情况下,另一个变量也是可以三分的,那么就可以用三分套三分求解,先三分一个值,然后在该值确定的情况下,三分另一个值,得到最优解传回来用于第一个三分,直到得到最优解。
例1,Line belt
Link
在一个二维平面上有两条线段 AB 和 CD,在 AB 上的移动速度是 P,在 CD 上是 Q,在平面上的其他区域以速度 R 移动。
问,从 A 到 D 需要多长时间?
0 < = A x , A y , B x , B y , C x , C y , D x , D y < = 1000 0<= Ax,Ay,Bx,By,Cx,Cy,Dx,Dy<=1000 0<=Ax,Ay,Bx,By,Cx,Cy,Dx,Dy<=1000
1 < = P , Q , R < = 10 1<=P,Q,R<=10 1<=P,Q,R<=10
思路
最佳的策略一定是从 A 点移动到线段 AB 的某个位置,然后到线段 CD 的某个位置接着到 D 点。
但是到哪个位置不知道,两个变量。
可以看出,整体的时间一定是先减少后增加的,最优解在中间的某个位置,所以整体是可以三分的。
同时,当在线段 AB 的位置确定的话,到达 CD 的某个位置后到 D 点所要的时间也是先减少后增加的,也可以三分求出最优解。
所以,可以三分到线段 AB 的位置,在该位置确定的情况下,三分到线段 CD 上的位置,得到此时最优解传回去用以第一个三分,最终得到最优解。
Code
//http://acm.hdu.edu.cn/showproblem.php?pid=3400
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
double x, y;
};
node a, b, c, d, e, f;
double P, Q, R;
double dis(node a, node b){
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
double check1(node e, node f)
{
return dis(e, f)/R + dis(f, d)/Q;
}
double check(node e)
{
double lx = c.x, ly = c.y, rx = d.x, ry = d.y;
for(int i=1;i<=500;i++)
{
double lmidx = lx + (rx - lx)/3, rmidx = rx - (rx - lx)/3;
double lmidy = ly + (ry - ly)/3, rmidy = ry - (ry - ly)/3;
if(check1(e, {
lmidx, lmidy}) > check1(e, {
rmidx, rmidy})) lx = lmidx, ly = lmidy;
else rx = rmidx, ry = rmidy;
}
return dis(a, e)/P + check1(e, {
lx, ly});
}
signed main(){
Ios;
cin >> T;
while(T--)
{
cin >> a.x >> a.y >> b.x >> b.y;
cin >> c.x >> c.y >> d.x >> d.y;
cin >> P >> Q >> R;
double lx = a.x, ly = a.y, rx = b.x, ry = b.y;
for(int i=1;i<=500;i++) //当复杂度不确定时,可以按照所剩余的时间设置三分次数
{
double lmidx = lx + (rx - lx)/3, rmidx = rx - (rx - lx)/3;
double lmidy = ly + (ry - ly)/3, rmidy = ry - (ry - ly)/3;
if(check({
lmidx, lmidy}) > check({
rmidx, rmidy})) lx = lmidx, ly = lmidy;
else rx = rmidx, ry = rmidy;
}
printf("%.2lf\n", check({
lx, ly}));
}
return 0;
}
例2,1420. 通电围栏
Link
在一个二维坐标系中,给定 n 个线段的端点坐标。
要求找到一个位置,使其到 n 个线段的距离之和最小。
1 ≤ n ≤ 150 , 1≤n≤150 , 1≤n≤150,
0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 100 0≤x_1,y_1,x_2,y_2≤100 0≤x1,y1,x2,y2≤100
思路
容易想到,在从最佳位置向外扩散的过程中,该位置到线段的距离之和不断增大,中间小,四周大,整体可以三分。
同时,当横坐标确定的情况下,对于纵坐标的位置也是中间小,两边大,纵坐标也可以三分。
所以,三分横坐标,在横坐标确定的情况下,三分纵坐标得到最优解,返回来用于继续判断。
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
struct node{
double x, y;
}st[N], en[N];
double bi(double x, double y){
if(fabs(x - y) < 1e-6) return 0;
if(x > y) return 1;
return -1;
}
double distoline(node p, node a, node b)
{
double ap = (b.x-a.x)*(p.x-a.x)+(b.y-a.y)*(p.y-a.y);
if(bi(ap, 0) <= 0) return sqrt((p.x-a.x)*(p.x-a.x)+(p.y-a.y)*(p.y-a.y));//×î¶ÌΪap
double ab = (b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y);
if(bi(ap, ab) >= 0) return sqrt((p.x-b.x)*(p.x-b.x)+(p.y-b.y)*(p.y-b.y));//×î¶ÌΪbp
double r = ap/ab;
double px = a.x+(b.x-a.x)*r;
double py = a.y+(b.y-a.y)*r;
return sqrt((p.x-px)*(p.x-px)+(p.y-py)*(p.y-py));//´¹Ïß¾àÀë
}
double check1(node p)
{
double sum = 0;
for(int i=1;i<=n;i++){
sum += distoline(p, st[i], en[i]);
}
return sum;
}
double check(double x, int k)
{
double l = 0, r = 100;
for(int i=1;i<=200;i++)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check1({
x, lmid}) > check1({
x, rmid})) l = lmid;
else r = rmid;
}
if(k) printf("%.1f %.1f\n", l, check1({
x, l}));
return check1({
x, l});
}
signed main(){
Ios;
cin >> n;
for(int i=1;i<=n;i++){
double x, y; cin >> x >> y;
st[i] = {
x, y};
cin >> x >> y;
en[i] = {
x, y};
}
double l = 0, r = 100;
for(int i=1;i<=200;i++)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid, 0) > check(rmid, 0)) l = lmid;
else r = rmid;
}
printf("%.1f ", l);
check(l, 1);
return 0;
}
真题
1,D Arithmetic Sequence (21济南站)
Link
给定长度为 n 的数列,每个位置都是整数。
每次操作可以使一个元素 +1 或 -1。
问,最小用多少次操作能将该数列变为等差数列?
1 ≤ n ≤ 2 × 1 0 5 , 0 ≤ ∣ a i ∣ ≤ 1 0 13 1≤n≤2×10^5,\ 0≤∣a_i∣≤10^{13} 1≤n≤2×105, 0≤∣ai∣≤1013
思路
这场比赛去打了,当时看到的时候没有一点思路,没有刷过三分专题,也没往三分上想。。
然后刷过三分之后再看这道题,第一眼感觉是,首项和公差都不知道,两个变量未知,而整体的答案是先减小后增大,就想三分套三分。先三分首项再三分公差,样例能过,但是交一发超时。
2e5 * 2log1e13 * 2log1e13 超过 1e9,只能挂一个 log,也就是说要优化掉一个三分。
公差肯定要三分,那么能不能把三分首项优化掉呢?
也就是说,在已知公差的情况下,能否O(n)求出变成等差数列的操作次数?
是可以的。
对于一个等差数列来说,其每一项分别为 a1, a1+d, a1+2d, a1+3d, …, a1+(n-1)d。
如果把后面的公差减掉,那么每一项都是 a1。
而现在如果把当前的数列减去后面的公差,会得到n个数:x1, x2, x3, x4, …, xn。
这 n 个数其实应该是相同的,都是首项。
也就是要确定一个数,让这 n 个数都变成这个数的操作次数最少,也就是要找一个 t,使得: ∣ x 1 − t ∣ + ∣ x 2 − t ∣ + ∣ x 3 − t ∣ + . . . + ∣ x n − t ∣ |x_1-t| + |x_2-t| + |x_3-t| + ... + |x_n - t| ∣x1−t∣+∣x2−t∣+∣x3−t∣+...+∣xn−t∣ 最小。
货仓选址问题,最佳的 t 为这 n 个数的中位数,找到中位数便是首项,绝对值之和便是操作次数。
那么如何 O(n) 求中位数呢?可以用 nth_element()函数。
for(int i=0;i<n;i++) cin >> a[i];
nth_element(a, a+k, a+n); //使第k小整数就位
cout << a[k]; //调用第k小整数
或者
for(int i=1;i<=n;i++) cin >> a[i];
nth_element(a+1, a+k, a+n+1);//使第k小整数就位
cout << a[k]; //调用第k小整数
另外注意可能爆 long long,要用 __int128。
Code
//https://pintia.cn/problem-sets/1459829212832296960/problems/1459829264400629763
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define ll __int128
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
ll b[N];
ll check(int mid)
{
ll st = mid;
for(int i=1;i<=n;i++)
{
b[i] = a[i] - st;
st += mid;
}
nth_element(b+1, b+(n+1)/2, b+n+1);
int ans = b[(n+1)/2];
ll sum = 0;
for(int i=1;i<=n;i++){
if(b[i] > ans) sum += b[i] - ans;
else sum += ans - b[i];
}
return sum;
}
void print(ll x)
{
if(x > 9) print(x / 10);
putchar('0' + x % 10);
}
signed main(){
scanf("%lld", &n);
for(int i=1;i<=n;i++) scanf("%lld", &a[i]);
int l = -2e13, r = 2e13;
while(l < r)
{
int lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid + 1;
else r = rmid - 1;
}
print(check(l));
return 0;
}
2,Link with Arithmetic Progression (22牛客多校)
Link
给定长度为 n 的数列。
每次操作可以修改其中一个元素,花费为 ( a i − a i ′ ) 2 (a_i−a_i^′)^2 (ai−ai′)2。(可以修改为任意实数)
问,将数列变为等差数列的最小花费?
1 ≤ T ≤ 1000 , 3 ≤ n ≤ 1 0 5 , ∣ a i ∣ ≤ 1 0 9 , ∑ n < 1 e 6 1≤T≤1000,\ 3≤n≤10^5,\ |a_i| \leq 10^9, \sum n < 1e6 1≤T≤1000, 3≤n≤105, ∣ai∣≤109,∑n<1e6
思路
题目和上一题很类似,同样三分公差,然后 O(n) 求出最小花费。
同样,都减去后面的公差后,变为 x1, x2, x3, …, xn。
现在我们要使得 ( x 1 − t ) 2 + ( x 2 − t ) 2 + ( x 3 − t ) 2 + . . . + ( x n − t ) 2 (x_1 - t)^2 + (x_2 - t)^2 + (x_3 - t)^2 + ... + (x_n - t)^2 (x1−t)2+(x2−t)2+(x3−t)2+...+(xn−t)2 最小。
而 x i x_i xi 已知,所以上式就是一个开口向上的二次函数,直接找对称轴求最小值或者用 4 a c − b 2 4 a \frac {4ac-b^2} {4a} 4a4ac−b2。
或者,从上式直接看出将 t 赋值为 x i x_i xi 总和的平均值时最优。
比较奇怪的是,double 超时,换成 long double 就过了。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define PII pair<int,int>
#define endl '\n'
#define double long double
const int N = 200010, mod = 1e9+7;
int T, n, m;
double a[N], t[N], c[N];
namespace GTI
{
char gc(void)
{
const int S = 1 << 16;
static char buf[S], *s = buf, *t = buf;
if (s == t) t = buf + fread(s = buf, 1, S, stdin);
if (s == t) return EOF;
return *s++;
}
int gti(void)
{
int a = 0, b = 1, c = gc();
for (; !isdigit(c); c = gc()) b ^= (c == '-');
for (; isdigit(c); c = gc()) a = a * 10 + c - '0';
return b ? a : -a;
}
}
using GTI::gti;
double check(double d)
{
double x = a[1], sum = 0;
for(int i=1;i<=n;i++)
{
t[i] = a[i] - x;
x += d;
sum += t[i];
}
// sum /= n;
//
// double ans = 0;
// for(int i=1;i<=n;i++)
// ans += (t[i] - sum) * (t[i] - sum);
// return ans;
double a = 0, b = 0, c = 0;
for(int i=1;i<=n;i++)
{
a ++;
b -= 2*t[i];
c += t[i] * t[i];
}
// double ans = -b/(2*a);
// return a*ans*ans + b*ans + c;
return c - b*b/(4*a);
}
signed main(){
cin >> T;
while(T--)
{
n = gti();
for(int i=1;i<=n;i++) a[i] = gti();
double l = -1e9, r = 1e9;
while(fabs(r - l) > 1e-10)
{
double lmid = l + (r-l)/3, rmid = r - (r-l)/3;
if(check(lmid) > check(rmid)) l = lmid;
else r = rmid;
}
printf("%.10Lf\n", check(l));
}
return 0;
}
总结
总之,三分就是用于,在不确定最优解位置,但确实有峰值的情况下,求出最优解。
时间复杂度 O ( 2 l o g 3 n ) O(2log_3^n) O(2log3n)。
智能推荐
攻防世界_难度8_happy_puzzle_攻防世界困难模式攻略图文-程序员宅基地
文章浏览阅读645次。这个肯定是末尾的IDAT了,因为IDAT必须要满了才会开始一下个IDAT,这个明显就是末尾的IDAT了。,对应下面的create_head()代码。,对应下面的create_tail()代码。不要考虑爆破,我已经试了一下,太多情况了。题目来源:UNCTF。_攻防世界困难模式攻略图文
达梦数据库的导出(备份)、导入_达梦数据库导入导出-程序员宅基地
文章浏览阅读2.9k次,点赞3次,收藏10次。偶尔会用到,记录、分享。1. 数据库导出1.1 切换到dmdba用户su - dmdba1.2 进入达梦数据库安装路径的bin目录,执行导库操作 导出语句:./dexp cwy_init/[email protected]:5236 file=cwy_init.dmp log=cwy_init_exp.log 注释: cwy_init/init_123..._达梦数据库导入导出
js引入kindeditor富文本编辑器的使用_kindeditor.js-程序员宅基地
文章浏览阅读1.9k次。1. 在官网上下载KindEditor文件,可以删掉不需要要到的jsp,asp,asp.net和php文件夹。接着把文件夹放到项目文件目录下。2. 修改html文件,在页面引入js文件:<script type="text/javascript" src="./kindeditor/kindeditor-all.js"></script><script type="text/javascript" src="./kindeditor/lang/zh-CN.js"_kindeditor.js
STM32学习过程记录11——基于STM32G431CBU6硬件SPI+DMA的高效WS2812B控制方法-程序员宅基地
文章浏览阅读2.3k次,点赞6次,收藏14次。SPI的详情简介不必赘述。假设我们通过SPI发送0xAA,我们的数据线就会变为10101010,通过修改不同的内容,即可修改SPI中0和1的持续时间。比如0xF0即为前半周期为高电平,后半周期为低电平的状态。在SPI的通信模式中,CPHA配置会影响该实验,下图展示了不同采样位置的SPI时序图[1]。CPOL = 0,CPHA = 1:CLK空闲状态 = 低电平,数据在下降沿采样,并在上升沿移出CPOL = 0,CPHA = 0:CLK空闲状态 = 低电平,数据在上升沿采样,并在下降沿移出。_stm32g431cbu6
计算机网络-数据链路层_接收方收到链路层数据后,使用crc检验后,余数为0,说明链路层的传输时可靠传输-程序员宅基地
文章浏览阅读1.2k次,点赞2次,收藏8次。数据链路层习题自测问题1.数据链路(即逻辑链路)与链路(即物理链路)有何区别?“电路接通了”与”数据链路接通了”的区别何在?2.数据链路层中的链路控制包括哪些功能?试讨论数据链路层做成可靠的链路层有哪些优点和缺点。3.网络适配器的作用是什么?网络适配器工作在哪一层?4.数据链路层的三个基本问题(帧定界、透明传输和差错检测)为什么都必须加以解决?5.如果在数据链路层不进行帧定界,会发生什么问题?6.PPP协议的主要特点是什么?为什么PPP不使用帧的编号?PPP适用于什么情况?为什么PPP协议不_接收方收到链路层数据后,使用crc检验后,余数为0,说明链路层的传输时可靠传输
软件测试工程师移民加拿大_无证移民,未受过软件工程师的教育(第1部分)-程序员宅基地
文章浏览阅读587次。软件测试工程师移民加拿大 无证移民,未受过软件工程师的教育(第1部分) (Undocumented Immigrant With No Education to Software Engineer(Part 1))Before I start, I want you to please bear with me on the way I write, I have very little gen...
随便推点
Thinkpad X250 secure boot failed 启动失败问题解决_安装完系统提示secureboot failure-程序员宅基地
文章浏览阅读304次。Thinkpad X250笔记本电脑,装的是FreeBSD,进入BIOS修改虚拟化配置(其后可能是误设置了安全开机),保存退出后系统无法启动,显示:secure boot failed ,把自己惊出一身冷汗,因为这台笔记本刚好还没开始做备份.....根据错误提示,到bios里面去找相关配置,在Security里面找到了Secure Boot选项,发现果然被设置为Enabled,将其修改为Disabled ,再开机,终于正常启动了。_安装完系统提示secureboot failure
C++如何做字符串分割(5种方法)_c++ 字符串分割-程序员宅基地
文章浏览阅读10w+次,点赞93次,收藏352次。1、用strtok函数进行字符串分割原型: char *strtok(char *str, const char *delim);功能:分解字符串为一组字符串。参数说明:str为要分解的字符串,delim为分隔符字符串。返回值:从str开头开始的一个个被分割的串。当没有被分割的串时则返回NULL。其它:strtok函数线程不安全,可以使用strtok_r替代。示例://借助strtok实现split#include <string.h>#include <stdio.h&_c++ 字符串分割
2013第四届蓝桥杯 C/C++本科A组 真题答案解析_2013年第四届c a组蓝桥杯省赛真题解答-程序员宅基地
文章浏览阅读2.3k次。1 .高斯日记 大数学家高斯有个好习惯:无论如何都要记日记。他的日记有个与众不同的地方,他从不注明年月日,而是用一个整数代替,比如:4210后来人们知道,那个整数就是日期,它表示那一天是高斯出生后的第几天。这或许也是个好习惯,它时时刻刻提醒着主人:日子又过去一天,还有多少时光可以用于浪费呢?高斯出生于:1777年4月30日。在高斯发现的一个重要定理的日记_2013年第四届c a组蓝桥杯省赛真题解答
基于供需算法优化的核极限学习机(KELM)分类算法-程序员宅基地
文章浏览阅读851次,点赞17次,收藏22次。摘要:本文利用供需算法对核极限学习机(KELM)进行优化,并用于分类。
metasploitable2渗透测试_metasploitable2怎么进入-程序员宅基地
文章浏览阅读1.1k次。一、系统弱密码登录1、在kali上执行命令行telnet 192.168.26.1292、Login和password都输入msfadmin3、登录成功,进入系统4、测试如下:二、MySQL弱密码登录:1、在kali上执行mysql –h 192.168.26.129 –u root2、登录成功,进入MySQL系统3、测试效果:三、PostgreSQL弱密码登录1、在Kali上执行psql -h 192.168.26.129 –U post..._metasploitable2怎么进入
Python学习之路:从入门到精通的指南_python人工智能开发从入门到精通pdf-程序员宅基地
文章浏览阅读257次。本文将为初学者提供Python学习的详细指南,从Python的历史、基础语法和数据类型到面向对象编程、模块和库的使用。通过本文,您将能够掌握Python编程的核心概念,为今后的编程学习和实践打下坚实基础。_python人工智能开发从入门到精通pdf