数学建模十大算法02—插值与拟合(拉格朗日插值、三次样条插值、线性最小二乘法……)_三次插值与最小二乘法的关系-程序员宅基地
文章目录
引入
插值: 求过已知有限个数据点的近似函数。(强调这个近似函数要过所有已知点)
拟合: 已知有限个数据点,求近似函数,可不过已知数据点,只要求在某种意义下它在这些点上的总偏差最小。
插值和拟合都是要根据一组数据构造一个函数作为近似,由于近似的要求不同,二者的数学方法上是完全不同的。 而面对一个实际问题,究竟应该用插值还是拟合,有时容易确定,有时则并不明显。
一、插值
在工程和数学应用中,经常有这样一类数据处理问题,在平面上给定一组离散点列,要求一条曲线,把这些点按次序连接起来,称为插值。
我们为什么要进行插值呢?
我们进行数据处理的理想,当然是希望数据非常的完备,啥玩意儿都有。但现实往往不尽如人意,数据经常会缺东少西的,那怎么办呢?
我们需要对一些不存在的数据进行一些插补。比如,我们分析某个餐馆在一段时间内的营收情况,但某一天收银系统出问题了,这天都是手工收款入账的,我们的系统里面就没有这一天的营收数据。那怎么办呢?我们就需要根据一定的办法把这天的营收数据给找补回来,那怎么找补呢?常用的方法有:

已知 n + 1 n+1 n+1 个点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) ( i = 0 , 1 , . . . , n ) (i=0,1,...,n) (i=0,1,...,n),下面求各种插值函数。
1.1 分段线性插值
简单地说,将每两个相邻的节点用直线连起来,如此形成的一条折线就是分段线性插值函数。计算 x x x点的插值时,只用到 x x x左右的两个节点,计算量与节点个数 n n n无关。但 n n n越大,分段越多,插值误差越小。
假设两个节点为 ( x 1 , y 1 ) ( x 2 , y 2 ) \left(x_{1}, y_{1}\right)\left(x_{2}, y_{2}\right) (x1,y1)(x2,y2),则该区间上的一次线性方程为:

其证明过程非常简单:


以上就是分段线性插值的原理,可以看出原理十分简单。分段线性插值运算量较小,插值误差较小,插值函数具有连续性,但是由于在已知点的斜率是不变的,所以导致插值结果不光滑,存在角点。
该方法可用matlab自带的interp1函数实现。
x = 0:10; % 已知x值
y = x.*sin(x); % 已知y值(表达式)
x1 = 0:0.25:10; % 要求的插值点
y1 = interp1(x,y,x1); % 用一维插值方法求出的值,默认method为linear
plot(x,y,'k*',x1,y1)
其运行的结果如下所示:

实际上用函数表作插值计算时,分段线性插值就足够了,如数学、物理中用的特殊函数表,数理统计中用的概率分布表等。
1.2 牛顿插值法
首先我们要知道牛顿多项式的形式: N n ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) ( x − x 1 ) + ⋯ + a n ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) \mathrm{N}_{\mathrm{n}}(\mathrm{x})=\mathrm{a}_0+\mathrm{a}_1\left(\mathrm{x}-\mathrm{x}_0\right)+\mathrm{a}_2\left(\mathrm{x}-\mathrm{x}_0\right)\left(\mathrm{x}-\mathrm{x}_1\right)+\cdots+\mathrm{a}_{\mathrm{n}}\left(\mathrm{x}-\mathrm{x}_0\right)\left(\mathrm{x}-\mathrm{x}_1\right) \cdots\left(\mathrm{x}-\mathrm{x}_{\mathrm{n}-1}\right) Nn(x)=a0+a1(x−x0)+a2(x−x0)(x−x1)+⋯+an(x−x0)(x−x1)⋯(x−xn−1)
其中 a k ( k = 0 , 1 , . . . , n ) a_k (k=0,1,...,n) ak(k=0,1,...,n)为待定系数。
自变量之差与因变量之差之比叫差商。
定义: 函数 y = f ( x ) \mathrm{y}=\mathrm{f}(\mathrm{x}) y=f(x) 在区间 [ x i , x i + 1 ] \left[\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right] [xi,xi+1] 上的平均变化率
f [ x i , x i + 1 ] = f ( x i + 1 ) − f ( x i ) x i + 1 − x i \mathrm{f}\left[\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right]=\frac{\mathrm{f}\left(\mathrm{x}_{\mathrm{i}+1}\right)-\mathrm{f}\left(\mathrm{x}_{\mathrm{i}}\right)}{\mathrm{x}_{\mathrm{i}+1}-\mathrm{x}_{\mathrm{i}}} f[xi,xi+1]=xi+1−xif(xi+1)−f(xi)
称为 f ( x ) f(x) f(x) 关于 x i , x i + 1 x_i, x_{i+1} xi,xi+1 的一阶差商,并记为 f [ x i , x i + 1 ] f\left[x_i, x_{i+1}\right] f[xi,xi+1]
二阶差商:
f [ x i , x i + 1 , x i + 2 ] = f [ x i + 1 , x i + 2 ] − f [ x i , x i + 1 ] x i + 2 − x i \mathrm{f}\left[\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}, \mathrm{x}_{\mathrm{i}+2}\right]=\frac{\mathrm{f}\left[\mathrm{x}_{\mathrm{i}+1}, \mathrm{x}_{\mathrm{i}+2}\right]-\mathrm{f}\left[\mathrm{x}_{\mathrm{i}}, \mathrm{x}_{\mathrm{i}+1}\right]}{\mathrm{x}_{\mathrm{i}+2}-\mathrm{x}_{\mathrm{i}}} f[xi,xi+1,xi+2]=xi+2−xif[xi+1,xi+2]−f[xi,xi+1]
m \mathrm{m} m 阶差商:
f [ x 0 , x 1 , ⋯ , x m ] = f [ x 1 , x 2 , ⋯ , x m ] − f [ x 0 , x 1 , ⋯ , x m − 1 ] x m − x 0 \mathrm{f}\left[\mathrm{x}_0, \mathrm{x}_1, \cdots, \mathrm{x}_{\mathrm{m}}\right]=\frac{\mathrm{f}\left[\mathrm{x}_1, \mathrm{x}_2, \cdots, \mathrm{x}_{\mathrm{m}}\right]-\mathrm{f}\left[\mathrm{x}_0, \mathrm{x}_1, \cdots, \mathrm{x}_{\mathrm{m}-1}\right]}{\mathrm{x}_{\mathrm{m}}-\mathrm{x}_0} f[x0,x1,⋯,xm]=xm−x0f[x1,x2,⋯,xm]−f[x0,x1,⋯,xm−1]
那么,牛顿插值公式为:
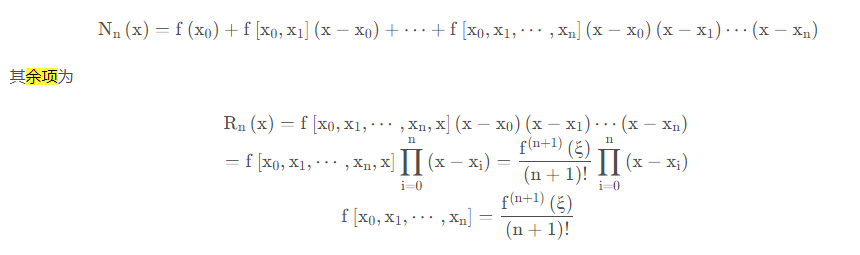
更多细节请参考:数值分析(一) 牛顿插值法及matlab代码
1.3 拉格朗日插值多项式
举个简单的例子,比如说,已知下面这几个点,我想找一根穿过它们的曲线:

我们可以合理的假设,这根曲线是一个二次多项式:

这是因为有三个已知的点,可以通过下列方程组解出这个二次多项式:

不过这里不打算通过解方程来得到这根二次曲线,如果已知的点有很多,那我们需要解的方程组会很复杂,因此我们来看看拉格朗日是怎么巧妙解出这根曲线的?
首先,第一根曲线 f 1 ( x ) f_1(x) f1(x),在 x 1 x_1 x1 点处,取值为1,其余两点取值为0:

第二根曲线 f 2 ( x ) f_2(x) f2(x),在 x 2 x_2 x2 点处,取值为1,其余两点取值为0:

第三根曲线 f 3 ( x ) f_3(x) f3(x),在 x 3 x_3 x3 点处,取值为1,其余两点取值为0:

这三根曲线就是拉格朗日需要的,我们来看看为什么?

那么 f ( x ) = y 1 f 1 ( x ) + y 2 f 2 ( x ) + y 3 f 3 ( x ) f(x) = y_1f_1(x) + y_2f_2(x) + y_3f_3(x) f(x)=y1f1(x)+y2f2(x)+y3f3(x) 这个方程就可以经过已知的三个点。
就可以穿过这三个点,用一个动图直观理解下:

最终得到的曲线就是拉格朗日找到的曲线:

用严格的数学表达来理解拉格朗日插值法,过程如下:
拉格朗日(Lagrange)插值的基函数为: l i ( x ) = ( x − x 0 ) ⋯ ( x − x i − 1 ) ( x − x i + 1 ) ⋯ ( x − x n ) ( x i − x 0 ) ⋯ ( x i − x i − 1 ) ( x i − x i + 1 ) ⋯ ( x i − x n ) = ∏ j = 0 j ≠ i n x − x j x i − x j , i = 0 , 1 , ⋯ , n ∘ \begin{aligned} l_i(x) &=\frac{\left(x-x_0\right) \cdots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right) \cdots\left(x-x_n\right)}{\left(x_i-x_0\right) \cdots\left(x_i-x_{i-1}\right)\left(x_i-x_{i+1}\right) \cdots\left(x_i-x_n\right)} \\ &=\prod_{\substack{j=0 \\ j \neq i}}^n \frac{x-x_j}{x_i-x_j}, i=0,1, \cdots, n_{\circ} \end{aligned} li(x)=(xi−x0)⋯(xi−xi−1)(xi−xi+1)⋯(xi−xn)(x−x0)⋯(x−xi−1)(x−xi+1)⋯(x−xn)=j=0j=i∏nxi−xjx−xj,i=0,1,⋯,n∘
l i ( x ) l_{i}(x) li(x)是 n n n次多项式,满足
l i ( x j ) = { 0 , j ≠ i 1 , j = i ∘ l_i\left(x_j\right)=\left\{\begin{array}{l} 0, j \neq i \\ 1, j=i_{\circ} \end{array}\right. li(xj)={
0,j=i1,j=i∘
拉格朗日插值函数为:
L n ( x ) = ∑ i = 0 n y i l i ( x ) = ∑ i = 0 n y i ( ∏ j = 0 j ≠ i n x − x j x i − x j ) L_n(x)=\sum_{i=0}^n y_i l_i(x)=\sum_{i=0}^n y_i\left(\prod_{\substack{j=0 \\ j \neq i}}^n \frac{x-x_j}{x_i-x_j}\right) Ln(x)=i=0∑nyili(x)=i=0∑nyi⎝
⎛j=0j=i∏nxi−xjx−xj⎠
⎞
我们可以将给定的 n + 1 n+1 n+1 个点带入拉格朗日基本多项式(插值基函数),发现当且仅当 i = j i=j i=j 时取1,其余情况取0,这样就保证了 L L L 经过这 n + 1 n+1 n+1 个点。
matlab代码如下:
function y0=Lagrange(x,y,x0)
n=length(x);
l=ones(1,n);
y0=0;
for j=1:n
for k=1:n
if j~=k % j≠k时
l(j)=l(j)*(x0-x(k))/(x(j)-x(k));
end
end
end
for i=1:n
y0=y0+l(i)*y(i);
end
1.4 样条插值
许多工程技术中提出的计算问题对插值函数的光滑性有较高要求,如飞机的机翼外形,内燃机的进、排气门的凸轮曲线,都要求曲线具有较高的光滑程度,不仅要连续,而且要有连续的曲率,这就导致了样条插值的产生。
样条(Spline) 本来是工程设计中使用的一种绘图工具,是富有弹性的细木条或细金属条。绘图员利用它把一些已知点连接成一条光滑曲线(称为样条曲线),并使连接点处有连续的曲率。三次样条插值就是由此抽象而来的。
简单来说,样条插值就是根据每两个相邻的数据点确定一段函数,然后再结合成一个函数,那么就是光滑的函数了。

数学上将具有一定光滑性的分段多项式称为样条函数。具体地说,给定区间[a,b]的一个分划:

如果函数 S ( x ) S(x) S(x) 满足:

1.4.1 三次样条插值
利用样条函数进行插值,即取插值函数为样条函数,称为样条插值。例如分段线性插值是一次样条插值。这里只介绍三次样条插值,即已知函数 y = f ( x ) y=f(x) y=f(x) 在区间 [ a , b ] [a,b] [a,b] 上的 n + 1 n+1 n+1 个节点 a = x 0 < x 1 < ⋯ < x n − 1 < x n = b a=x_0<x_1<\cdots<x_{n-1}<x_n=b a=x0<x1<⋯<xn−1<xn=b 上的值 y i = f ( x i ) ( i = 0 , 1... , n ) y_i = f(x_i) (i=0,1...,n) yi=f(xi)(i=0,1...,n) ,求插值函数 S ( x ) S(x) S(x) ,使得:


Matlab中三次样条插值有如下函数:
y = interp1(xdata,ydata,x,'spline');
y = spline(xdata,ydata,x);
pp = csape(x0,y0,conds); y = fnval(pp,x);
pp = csape(x0,y0,conds,valconds); y = fnval(pp,x);
pp = csape(x0,y0)使用默认的边界条件,即Lagrange边界条件。
pp = csape(x0,y0,conds,valconds)中的conds的指定插值的边界条件,其值可为:
- ‘complete’ 边界为一阶导数,一阶导数的值在valconds参数中给出,若忽略valconds参数视为默认情况。
- 'second’边界为二阶导数,二阶导数的值在参数valconds中给出,不使用参数valconds,默认值为[0,0]。

1.5 二维插值
前面讲述的都是一维插值,即节点为一维变量,插值函数是一元函数(曲线)。若节点是二维的,插值函数就是二元函数,即曲面。 如在某区域测量了若干点(节点)的高程(节点值),为了画出较精确的等高线图,就要先插入更多的点(插值点),计算这些点的高程(插值)。
1.5.1 插值节点为网格节点

Matlab中计算二维插值的命令如下:
z = interp2(x0,y0,z0,x,y,'method')
其中: x 0 x_0 x0, y 0 y_0 y0 分别为 m m m 维和 n n n 维向量,表示节点; z 0 z_0 z0为 n × m n×m n×m 矩阵,表示节点值; x x x, y y y 为一维数组,表示插值点, x x x与 y y y应是方向不同的向量,即一个是行向量,另一个是列向量; z z z为矩阵,它的行数为 y y y的维数,列数为 x x x的维数,表示得到的插值;'method’的用法同上面的一维插值。

【例】 测得平板表面3×5网格点处的温度分别为:

试作出平板表面温度分布曲面 z = f ( x , y ) z=f(x,y) z=f(x,y)的图形。
第一步:先在三维坐标画出原始数据,画出粗糙的温度分布曲面。
x=1:5;
y=1:3;
temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
mesh(x,y,temps) % 构建空间曲面图(mesh画的是曲线网格图,surf画的是曲面网格图)
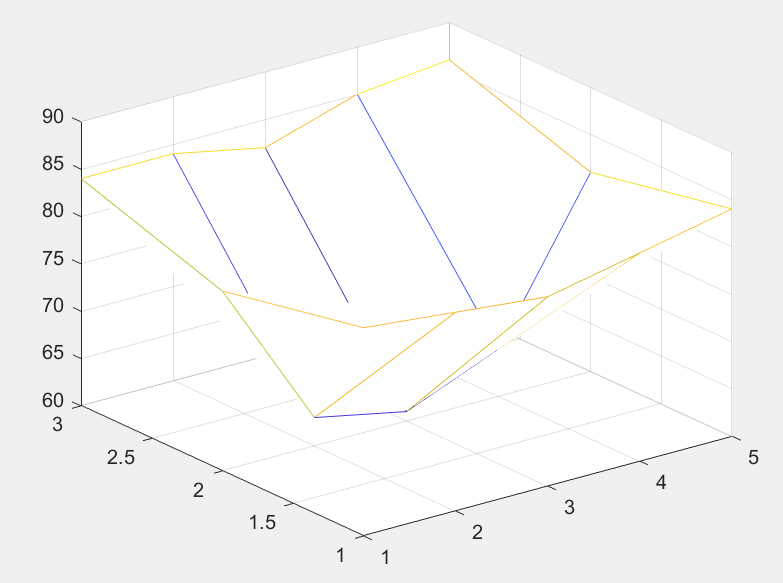
第二步:以平滑数据,在x、y方向上每隔0.2个单位的地方进行插值。
xi=1:0.2:5;
yi=1:0.2:3;
zi=interp2(x,y,temps,xi',yi,'cubic'); % 注意这里x和y形状不一样,任意一个作为行向量,另一个作为列向量
mesh(xi,yi,zi)

用contour(xi,yi,zi,20,'r')作其等高线图(等高线图:z值一样的点连起来的图)如下:

如果是三次样条插值,可以使用命令:
pp = csape({
x0,y0},z0,conds,valconds);
z = fnval(pp,{
x,y});
其中: x 0 x_0 x0, y 0 y_0 y0 分别为 m m m 维和 n n n 维向量; z 0 z_0 z0为 m × n m×n m×n 矩阵; z z z为矩阵,它的行数为 x x x的维数,列数为 y y y的维数,表示得到的插值,具体使用方法同一维插值。
1.5.2 插值节点为散乱节点
注意此时已知的是n个节点,和1.5.1的m×n个节点情况不同。
对上述问题,Matlab中提供了插值函数griddata,其格式为:
ZI = griddata(x,y,z,XI,YI);
【例】 在某海域测得一些点 ( x , y ) (x,y) (x,y)处的水深z由下表给出,船的吃水深度为5英尺,在矩形区域 ( 75 , 200 ) × ( − 50 , 150 ) (75,200) ×(-50,150) (75,200)×(−50,150) 里的哪些地方船要避免进入。在矩形区域内画出海底曲面的图形。

由题意得,船的吃水深度小于5米时,船比较容易搁浅。
x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];
cx=75:0.5:200; % 矩形区域
cy=-50:0.5:150;
cz=griddata(x,y,z,cx,cy','cubic'); % 采用立方插值在矩形区域内做二维插值
figure(1),meshz(cx,cy,cz); % 海底曲线图
xlabel('X'),ylabel('Y'),zlabel('Z');

figure(2),contour(cx,cy,cz,[-5 -5],'r'); % 画出深度为5米的等高线,则在等高线内部的深度均小于5米
grid;
hold on;
plot(x,y,'+'); % 二维坐标中标出数据各个点位置
xlabel('X'),ylabel('Y');

红色曲线内部的点都是船比较容易搁浅的位置。
1.6 例题
【例】机床加工。 待加工零件的外形根据工艺要求由一组数据 ( x , y ) (x,y) (x,y) 给出(在平面情况下),用程控铣床加工时每一刀只能沿 x x x 方向和 y y y 方向走非常小的一步,这就需要从已知数据得到加工所要求的步长很小的 ( x , y ) (x,y) (x,y) 坐标。
表5.1中给出的 x , y x,y x,y 数据位于机翼断面的下轮廓线上,假设需要得到 x x x 坐标每改变0.1时的 y y y 坐标。试完成加工所需数据,画出曲线,要求用最近项插值、分段线性插值和三次样条插值(不同边界)方法计算。

Matlab代码如下:
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
% ------最近项插值
y1 = interp1(x0,y0,x,'nearest');
subplot(1,5,1)
plot(x0,y0,'+',x,y1);
title('nearest method');
% ------ 线性插值
y2 = interp1(x0,y0,x);
subplot(1,5,2)
plot(x0,y0,'+',x,y2);
title('Piecewise linear');
% ------立方样条插值
y3 = interp1(x0,y0,x,'spline');
subplot(1,5,3)
plot(x0,y0,'+',x,y3)
title('Splinel')
% ------三次样条插值的Lagrange边界条件
pp1 = csape(x0,y0);
y4 = fnval(pp1,x);
subplot(1,5,4)
plot(x0,y0,'+',x,y4)
title('Spline2')
% ------指定插值边界条件为二阶导数
pp2 = csape(x0,y0,'second');
y5 = fnval(pp2,x); % 使用fnval函数求插值点的函数值
subplot(1,5,5)
plot(x0,y0,'+',x,y5);
title('Spline3')
其运行结果为:

我们可以明显感觉到,三次样条插值得到的曲线会更加平滑。
【例】 在某山区测得一些地点的高程如下表。平面区域为 1200 ≤ x ≤ 4000 , 1200 ≤ y < 3600 1200≤x≤4000, 1200≤y<3600 1200≤x≤4000,1200≤y<3600,试用Matlab中的最邻近插值、双线性插值和双三次插值3种方法作出该山区的地貌图和等高线图,并求出最高和最低点,并对几种插值方法进行比较。

首先,第一步我们做出已知点的网格面。
x=1200:400:4000;
y=1200:400:3600;
[xx,yy]=meshgrid(x,y); % xx是以x为行(列数为向量x的长度)的矩阵,yy是以y为列(行数为y的长度)的矩阵。[xx,yy]矩阵x和矩阵y合在一起
z=[1130 1250 1280 1230 1040 900 500 700; 1320 1450 1420 1400 1300 700 900 850;
1390 1500 1500 1400 900 1100 1060 950; 1500 1200 1100 1350 1450 1200 1150 1010;
1500 1200 1100 1550 1600 1550 1380 1070; 1500 1550 1600 1550 1600 1600 1600 1550;
1480 1500 1550 1510 1430 1300 1200 980];
figure(1);
meshz(x,y,z)
xlabel('X'),ylabel('Y'),zlabel('Z')
title('网格面')

然后,我们用最邻近插值法看一下插值结果:
xi=1200:40:4000;
yi=1200:40:3600;
figure(2)
z1i=interp2(x,y,z,xi,yi','nearest');
subplot(1,2,1),surfc(xi,yi,z1i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('最邻近插值');
subplot(1,2,2),contour(xi,yi,z1i,10,'r'),title('最邻近插值等高线图');

同样,看一下线性插值法及其等高线图。
figure(3)
z2i=interp2(x,y,z,xi,yi','linear');
subplot(1,2,1),surfc(xi,yi,z2i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('线性插值');
subplot(1,2,2),contour(xi,yi,z2i,10,'r'),title('线性插值等高线图');

立方插值法及其等高线图:
figure(4)
z3i=interp2(x,y,z,xi,yi','cubic');
subplot(1,2,1),surfc(xi,yi,z3i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('立方插值');
subplot(1,2,2),contour(xi,yi,z3i,10,'r'),title('立方插值等高线图');

三次样条插值法及等高线图:
figure(5)
z4i=interp2(x,y,z,xi,yi','spline');
subplot(1,2,1),surfc(xi,yi,z4i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('三次样条插值');
subplot(1,2,2),contour(xi,yi,z4i,10,'r'),title('三次样条插值等高线图');

分段线性插值法及其等高线图:
figure(6)
z5i=interp2(x,y,z,xi,yi');
subplot(1,2,1),surfc(xi,yi,z5i),xlabel('X'),ylabel('Y'),zlabel('Z'),title('分段线性插值');
subplot(1,2,2),contour(xi,yi,z5i,10,'r'),title('分段线性插值等高线图');

比较由以上五种插值方法得到的地貌图和等高线图,可以看出:
- 由于两个高度之间直线为最短距离,因此利用最邻近插值得到的地貌图和等高线为直线,描述的山地地貌皆为陡崖,对于一般山区的地貌是不符合的;
- 分段线性插值得到的图像随着分段数目的增多,而更加平缓,棱角更加不明显。
- 利用线性插值、三次样条插值和立方插值所得到的图像较为平滑,更加适合描述该山地的地貌。
二、拟合
2.1 曲线拟合的线性最小二乘法

原则上不需要经过图像中的任何一个点,只要保证与各点的距离总体足够小即可。
线性最小二乘法是解决曲线拟合最常用的方法,其基本思路是,令

拟合的准则是使 y i y_i yi 与 f ( x i ) f(x_i) f(xi) 的距离的平方和最小,称为最小二乘法。
那么,系数 a k a_k ak该怎么确定呢?这里参考了《数学建模算法与应用》的证明过程。
1)系数 a k a_k ak的确定


2)函数 r k ( x ) r_k(x) rk(x)的选取
面对一组数据 ( x i , y i ) (x_i,y_i) (xi,yi), i = 1 , 2 , . . . , n i=1 ,2,...,n i=1,2,...,n,用线性最小二乘法作曲线拟合时,首要的也是关键的一步是恰当地选取 r 1 ( x ) , . . , r m ( x ) r_1(x),..,r_m (x) r1(x),..,rm(x) 。如果通过机理分析,能够知道y与x之间的函数关系, 则 r 1 ( x ) , . . , r m ( x ) r_1(x),..,r_m (x) r1(x),..,rm(x) 容易确定。若无法知道 y y y 与 x x x 之间的关系,通常可以将数据 ( x i , y i ) (x_i,y_i) (xi,yi), i = 1 , 2 , . . . , n i=1 ,2,...,n i=1,2,...,n 作图,直观地判断应该用什么样的曲线去作拟合。常用的曲线有如下:

已知一组数据,用什么样的曲线拟合最好,可以在直观判断的基础上,选几种曲线分
别拟合,然后比较,看哪条曲线的最小二乘指标 J J J 最小。
在Matlab中,线性最小二乘法的标准型为:

【例】 用最小二乘法求一个形如 y = a + b x 2 y=a+bx^2 y=a+bx2 的经验公式,拟合下表中的数据。

X=[19 25 31 38 44]';
Y=[19.0 32.3 49.0 73.3 97.8]';
R=[ones(5,1),x.^2]
我们看一下这里R的值,进一步理解上文推导过程中的含义:

用Matlab标准型的命令求系数:
ab=R\Y
求得的结果如下:

意味着,求得的拟合公式为: y = 0.9726 + 0.05 x 2 y=0.9726 + 0.05x^2 y=0.9726+0.05x2。
我们来看一下该曲线的拟合效果如何?
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(X,Y,'o',x0,y0,'r')

注:这里可以联想到GM(1,1)模型中用到了最小二乘法。
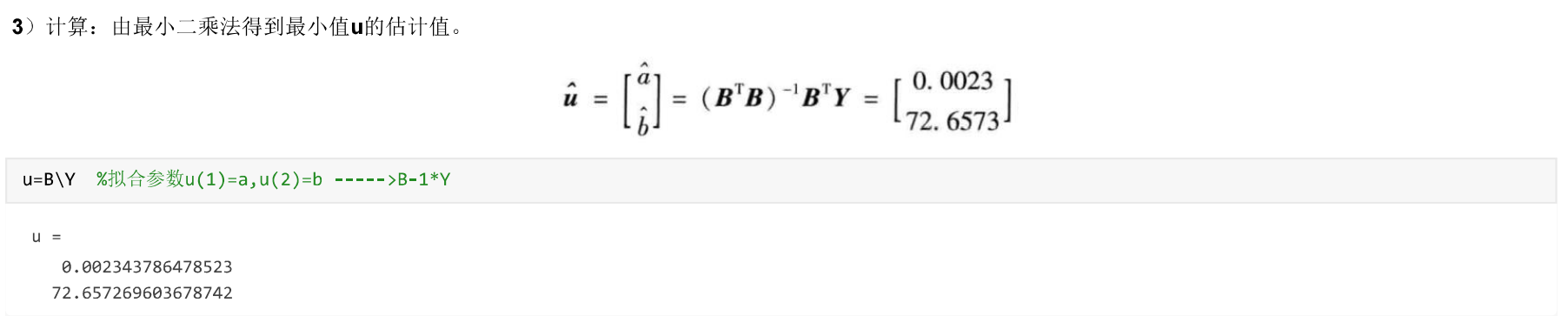
2.2 多项式拟合
如果取

即用 m m m 次多项式拟合给定数据,MatLab中有现成的函数a=polyfit(x0,y0,m)。
其中,输入参数 x 0 、 y 0 x_0、y_0 x0、y0 为要拟合的数据; m m m 为拟合多项式的次数。输出参数 a a a 为拟合多项式的系数向量。
【例】 某乡镇企业1990年—1996年的生产利润如表所列。

试预测1997年和1998年的利润。
思路如下:
首先第一步我们可以作已知数据的散点图,直观判断其需要什么样的多项式拟合。
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
plot(x0,y0,'*')

我们可以发现,该乡镇企业的年生产利润几乎直线上升。因此,可以用 y = a 1 x + a 0 y=a_1x+a_0 y=a1x+a0 作为拟合函数来预测该乡镇企业未来的年利润。代码如下:
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
a=polyfit(x0,y0,1)
y97=polyval(a,1997)
y98=polyval(a,1998)
最终求得的结果为:(注意,次数高的项在前面)


2.3 指定函数拟合
fittype是自定义拟合函数,cfun=fit(x,y,f)。拟合数据 x 、 y x、y x、y 必须为列向量。
假设原始数据散点图如下所示:

我们可以编写一个m文件来实现自定义拟合函数。
syms t
x = [0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y = [1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
f = fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{
'a','k','w'});
cfun = fit(x,y,f) %显示拟合函数
xi = 0:.1:20;
yi = cfun(xi);
plot(x,y,'r*',xi,yi,'b-');

求出来系数 a 、 k 、 w a、k、w a、k、w 的值分别为:

三、综合案例

先挖一个坑在这,有空再来写。
参考文章
[1] 插值算法——分段线性插值(1)
[2] 如何直观地理解拉格朗日插值法?(知乎)
[3] 数值分析(一) 牛顿插值法及matlab代码
[4] 数值分析(二) 三次样条插值法matlab程序
[5] 数学建模学习-插值法
[6] 数学建模——拟合
智能推荐
使用nginx解决浏览器跨域问题_nginx不停的xhr-程序员宅基地
文章浏览阅读1k次。通过使用ajax方法跨域请求是浏览器所不允许的,浏览器出于安全考虑是禁止的。警告信息如下:不过jQuery对跨域问题也有解决方案,使用jsonp的方式解决,方法如下:$.ajax({ async:false, url: 'http://www.mysite.com/demo.do', // 跨域URL ty..._nginx不停的xhr
在 Oracle 中配置 extproc 以访问 ST_Geometry-程序员宅基地
文章浏览阅读2k次。关于在 Oracle 中配置 extproc 以访问 ST_Geometry,也就是我们所说的 使用空间SQL 的方法,官方文档链接如下。http://desktop.arcgis.com/zh-cn/arcmap/latest/manage-data/gdbs-in-oracle/configure-oracle-extproc.htm其实简单总结一下,主要就分为以下几个步骤。..._extproc
Linux C++ gbk转为utf-8_linux c++ gbk->utf8-程序员宅基地
文章浏览阅读1.5w次。linux下没有上面的两个函数,需要使用函数 mbstowcs和wcstombsmbstowcs将多字节编码转换为宽字节编码wcstombs将宽字节编码转换为多字节编码这两个函数,转换过程中受到系统编码类型的影响,需要通过设置来设定转换前和转换后的编码类型。通过函数setlocale进行系统编码的设置。linux下输入命名locale -a查看系统支持的编码_linux c++ gbk->utf8
IMP-00009: 导出文件异常结束-程序员宅基地
文章浏览阅读750次。今天准备从生产库向测试库进行数据导入,结果在imp导入的时候遇到“ IMP-00009:导出文件异常结束” 错误,google一下,发现可能有如下原因导致imp的数据太大,没有写buffer和commit两个数据库字符集不同从低版本exp的dmp文件,向高版本imp导出的dmp文件出错传输dmp文件时,文件损坏解决办法:imp时指定..._imp-00009导出文件异常结束
python程序员需要深入掌握的技能_Python用数据说明程序员需要掌握的技能-程序员宅基地
文章浏览阅读143次。当下是一个大数据的时代,各个行业都离不开数据的支持。因此,网络爬虫就应运而生。网络爬虫当下最为火热的是Python,Python开发爬虫相对简单,而且功能库相当完善,力压众多开发语言。本次教程我们爬取前程无忧的招聘信息来分析Python程序员需要掌握那些编程技术。首先在谷歌浏览器打开前程无忧的首页,按F12打开浏览器的开发者工具。浏览器开发者工具是用于捕捉网站的请求信息,通过分析请求信息可以了解请..._初级python程序员能力要求
Spring @Service生成bean名称的规则(当类的名字是以两个或以上的大写字母开头的话,bean的名字会与类名保持一致)_@service beanname-程序员宅基地
文章浏览阅读7.6k次,点赞2次,收藏6次。@Service标注的bean,类名:ABDemoService查看源码后发现,原来是经过一个特殊处理:当类的名字是以两个或以上的大写字母开头的话,bean的名字会与类名保持一致public class AnnotationBeanNameGenerator implements BeanNameGenerator { private static final String C..._@service beanname
随便推点
二叉树的各种创建方法_二叉树的建立-程序员宅基地
文章浏览阅读6.9w次,点赞73次,收藏463次。1.前序创建#include<stdio.h>#include<string.h>#include<stdlib.h>#include<malloc.h>#include<iostream>#include<stack>#include<queue>using namespace std;typed_二叉树的建立
解决asp.net导出excel时中文文件名乱码_asp.net utf8 导出中文字符乱码-程序员宅基地
文章浏览阅读7.1k次。在Asp.net上使用Excel导出功能,如果文件名出现中文,便会以乱码视之。 解决方法: fileName = HttpUtility.UrlEncode(fileName, System.Text.Encoding.UTF8);_asp.net utf8 导出中文字符乱码
笔记-编译原理-实验一-词法分析器设计_对pl/0作以下修改扩充。增加单词-程序员宅基地
文章浏览阅读2.1k次,点赞4次,收藏23次。第一次实验 词法分析实验报告设计思想词法分析的主要任务是根据文法的词汇表以及对应约定的编码进行一定的识别,找出文件中所有的合法的单词,并给出一定的信息作为最后的结果,用于后续语法分析程序的使用;本实验针对 PL/0 语言 的文法、词汇表编写一个词法分析程序,对于每个单词根据词汇表输出: (单词种类, 单词的值) 二元对。词汇表:种别编码单词符号助记符0beginb..._对pl/0作以下修改扩充。增加单词
android adb shell 权限,android adb shell权限被拒绝-程序员宅基地
文章浏览阅读773次。我在使用adb.exe时遇到了麻烦.我想使用与bash相同的adb.exe shell提示符,所以我决定更改默认的bash二进制文件(当然二进制文件是交叉编译的,一切都很完美)更改bash二进制文件遵循以下顺序> adb remount> adb push bash / system / bin /> adb shell> cd / system / bin> chm..._adb shell mv 权限
投影仪-相机标定_相机-投影仪标定-程序员宅基地
文章浏览阅读6.8k次,点赞12次,收藏125次。1. 单目相机标定引言相机标定已经研究多年,标定的算法可以分为基于摄影测量的标定和自标定。其中,应用最为广泛的还是张正友标定法。这是一种简单灵活、高鲁棒性、低成本的相机标定算法。仅需要一台相机和一块平面标定板构建相机标定系统,在标定过程中,相机拍摄多个角度下(至少两个角度,推荐10~20个角度)的标定板图像(相机和标定板都可以移动),即可对相机的内外参数进行标定。下面介绍张氏标定法(以下也这么称呼)的原理。原理相机模型和单应矩阵相机标定,就是对相机的内外参数进行计算的过程,从而得到物体到图像的投影_相机-投影仪标定
Wayland架构、渲染、硬件支持-程序员宅基地
文章浏览阅读2.2k次。文章目录Wayland 架构Wayland 渲染Wayland的 硬件支持简 述: 翻译一篇关于和 wayland 有关的技术文章, 其英文标题为Wayland Architecture .Wayland 架构若是想要更好的理解 Wayland 架构及其与 X (X11 or X Window System) 结构;一种很好的方法是将事件从输入设备就开始跟踪, 查看期间所有的屏幕上出现的变化。这就是我们现在对 X 的理解。 内核是从一个输入设备中获取一个事件,并通过 evdev 输入_wayland