图像频率域分析之傅里叶变换_研究傅里叶时域图像时频率是不变的吗-程序员宅基地
技术标签: 计算机视觉 图像处理 Computer Vision
Overview
欢迎访问 持续更新:https://cgabc.xyz/posts/bcb5a7d3/
傅里叶变换基础
傅里叶级数
法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),即 任何周期信号都可以表示成一系列正弦信号的叠加
- 三角形式
f ( t ) = a 0 2 + ∑ k = 1 + ∞ [ a k c o s ( n ω t ) + b k s i n ( n ω t ) ] , a 0 2 = 1 T ∫ − T 2 T 2 f ( t ) d t f(t) = \frac{a_0}{2} + \sum_{k=1}^{+\infty} \big[ a_k cos (n \omega t) + b_k sin (n \omega t) \big], \quad \frac{a_0}{2} = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) dt f(t)=2a0+k=1∑+∞[akcos(nωt)+bksin(nωt)],2a0=T1∫−2T2Tf(t)dt
- 复指数形式
f ( t ) = 1 T ∑ n = − ∞ + ∞ [ ∫ − T 2 T 2 f ( τ ) e − j ω n τ d τ ] e j ω n t f(t) = \frac{1}{T} \sum_{n=-\infty}^{+\infty} [ \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)e^{-j\omega_n\tau} d\tau ] e^{j\omega_nt} f(t)=T1n=−∞∑+∞[∫−2T2Tf(τ)e−jωnτdτ]ejωnt
基波角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π , T T T 为 f ( t ) f(t) f(t) 的周期, j j j 为虚数单位
傅里叶积分
复指数形式
f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − j ω τ d τ ] e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} [ \int_{-\infty}^{+\infty} f(\tau)e^{-j\omega\tau} d\tau ] e^{j\omega t} d\omega f(t)=2π1∫−∞+∞[∫−∞+∞f(τ)e−jωτdτ]ejωtdω
傅里叶变换
一维连续傅里叶变换
正变换 为
F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − j ω t d t F(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-j\omega t} dt F(ω)=∫−∞+∞f(t)e−jωtdt
逆变换 为
f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} F(\omega) e^{j\omega t} d\omega f(t)=2π1∫−∞+∞F(ω)ejωtdω
一维离散傅里叶变换
正变换 为
F ( u ) = ∑ x = 0 M − 1 f ( x ) e − j 2 π u x M F(u) = \sum_{x=0}^{M-1} f(x) e^{-j2\pi \frac{ux}{M}} F(u)=x=0∑M−1f(x)e−j2πMux
则
F ( 0 ) = ∑ x = 0 M − 1 f ( x ) F(0) = \sum_{x=0}^{M-1} f(x) F(0)=x=0∑M−1f(x)
反变换 为
f ( x ) = 1 M ∑ u = 0 M − 1 F ( u ) e j 2 π u x M f(x) = \frac{1}{M} \sum_{u=0}^{M-1} F(u) e^{j2\pi \frac{ux}{M}} f(x)=M1u=0∑M−1F(u)ej2πMux
对于反变换式前的系数 1 M \frac{1}{M} M1 ,也可放在正变换中,只要保证正变换与反变换之前的系数乘积为 1 M \frac{1}{M} M1 即可。
二维离散傅里叶变换
正变换
二维离散傅里叶变换:
F [ f ( x , y ) ] = F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F[f(x,y)] = F(u,v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} F[f(x,y)]=F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)
当 ( u , v ) (u,v) (u,v) 等于 ( 0 , 0 ) (0,0) (0,0) 时,直流分量 为:
F ( 0 , 0 ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) F(0,0) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) F(0,0)=x=0∑M−1y=0∑N−1f(x,y)
幅度谱 为:
A ( u , v ) = ∣ F ( u , v ) ∣ = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 A(u,v) = |F(u,v)| = \sqrt{Real(u,v)^2 + Image(u,u)^2} A(u,v)=∣F(u,v)∣=Real(u,v)2+Image(u,u)2
功率谱 为:
P ( u , v ) = ∣ F ( u , v ) ∣ 2 = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 P(u,v) = |F(u,v)|^{2} = Real(u,v)^2 + Image(u,u)^2 P(u,v)=∣F(u,v)∣2=Real(u,v)2+Image(u,u)2
相位谱 为:
ϕ ( u , v ) = a r c t a n I m a g e ( u , v ) R e a l ( u , v ) \phi(u,v) = arctan \frac{Image(u,v)}{Real(u,v)} ϕ(u,v)=arctanReal(u,v)Image(u,v)
通过 幅度谱 和 相位谱,我们也能合成 其傅里叶变换(频谱):
F ( u , v ) = A ( u , v ) e j ϕ ( u , v ) = A ( c o s ϕ + j s i n ϕ ) (省略(u,v),应用 欧拉公式) = A c o s ϕ + j A s i n ϕ \begin{aligned} F(u,v) &= A(u,v)e^{j\phi(u,v)} \\ &= A( cos \phi + jsin \phi ) \quad \text{(省略(u,v),应用 欧拉公式)}\\ &= Acos\phi + jAsin\phi \end{aligned} F(u,v)=A(u,v)ejϕ(u,v)=A(cosϕ+jsinϕ)(省略(u,v),应用 欧拉公式)=Acosϕ+jAsinϕ
注意:
- 上面式子中的 j j j 为 虚数单位
- R e a l ( u , v ) Real(u,v) Real(u,v) 为 复数的 实部
- I m a g e ( u , v ) Image(u,v) Image(u,v) 为 复数的 虚部
反变换
f ( x , y ) = F − 1 ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) e j 2 π ( u x M + v y N ) f(x,y) = F^{-1}(u,v) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u,v) e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})} f(x,y)=F−1(u,v)=MN1u=0∑M−1v=0∑N−1F(u,v)ej2π(Mux+Nvy)
卷积
∫ − ∞ + ∞ f 1 ( τ ) f 2 ( t − τ ) d τ = f 1 ( t ) ∗ f 2 ( t ) \int_{-\infty}^{+\infty} f_1(\tau)f_2(t-\tau) d\tau = f_1(t) * f_2(t) ∫−∞+∞f1(τ)f2(t−τ)dτ=f1(t)∗f2(t)
卷积定理
函数卷积的傅立叶变换是函数傅立叶变换的乘积
- 时域卷积定理:时域内的卷积对应频域内的乘积
F [ f 1 ( t ) ∗ f 2 ( t ) ] = F 1 ( ω ) ⋅ F 2 ( ω ) F[f_1(t) * f_2(t)] = F_1(\omega) \cdot F_2(\omega) F[f1(t)∗f2(t)]=F1(ω)⋅F2(ω)
- 频域卷积定理:频域内的卷积对应时域内的乘积
F [ f 1 ( t ) ⋅ f 2 ( t ) ] = 1 2 π F 1 ( ω ) ∗ F 2 ( ω ) F[f_1(t) \cdot f_2(t)] = \frac{1}{2\pi} F_1(\omega) * F_2(\omega) F[f1(t)⋅f2(t)]=2π1F1(ω)∗F2(ω)
数字图像DFT
借用知乎大神Heinrich的一张图,来个感性认识:
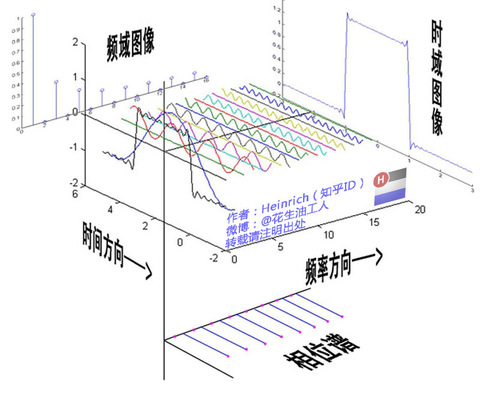
空间域和频域
- 空间域:在图像处理中,时域可以理解为 空间域 或者 图像空间,处理对象为图像像元;
- 频域:以 空间频率 为自变量描述图像的特征,可以将一幅图像像元值在空间上的变化分解为具有不同振幅、空间频率和相位的简振函数的线性叠加,图像中各种空间频率成分的组成和分布称为 图像频谱
空间域与频域可互相转换,对图像施行 二维离散傅立叶变换 或 小波变换 ,可以将图像由空间域转换到频域;通过 对应的反变换 又可转换回空间域图像,即人可以直接识别的图像。
图像频域滤波
二维数字图像的滤波主要分为 空间域滤波 和 频域滤波:
-
空间域滤波: 用各种模板直接与图像进行 卷积运算,实现对图像的处理,这种方法直接对图像空间操作,操作简单
-
频域滤波: 在实现某些图像处理的时候,频域的处理比空间域更简单;对于在空间域上的数字图像,根据 卷积定理 可以通过 傅立叶变换 将 空域卷积滤波 变换为 频域滤波,然后再将频域滤波处理后的图像 反变换 回空间域
基本步骤
图像频域滤波步骤为(频谱图中心化):
- 计算 原始图像 f ( x , y ) f(x,y) f(x,y) 的DFT,得到 频谱 F ( u , v ) F(u,v) F(u,v)
- 中心化:将频谱 F ( u , v ) F(u,v) F(u,v) 的零频点移动到频谱图的中心位置
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 反中心化:将频谱 G ( u , v ) G(u,v) G(u,v) 的零频点移回到频谱图的左上角位置
- 计算上一步计算结果的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部 作为最终滤波后的结果图像
上面步骤是对 图像频谱 进行 中心变换;我们也可以先对 原始图像 进行 中心变换,再计算其 频谱图,滤波步骤如下(原始图中心化):
- 原始图像 f ( x , y ) f(x,y) f(x,y) 中心变换: f ( x , y ) ⋅ ( − 1 ) ( x + y ) f(x,y) \cdot (-1)^{(x+y)} f(x,y)⋅(−1)(x+y)
- 计算上一步计算结果的DFT,得到其 频谱 F ( u , v ) F(u,v) F(u,v)
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 计算 G ( u , v ) G(u,v) G(u,v) 的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部
- 上一步计算结果 乘以 ( − 1 ) ( x + y ) (-1)^{(x+y)} (−1)(x+y) 作为最终滤波后的结果图像
滤波能否取得理想结果的关键取决于上面的 滤波器函数 H ( u , v ) H(u,v) H(u,v) 。
这时让我想到了《自动控制理论》中的 传递函数 G ( s ) G(s) G(s),定义为:初始条件为零的线性定常系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。
下面以 控制论的思想 给出图像频域滤波的示意框图:
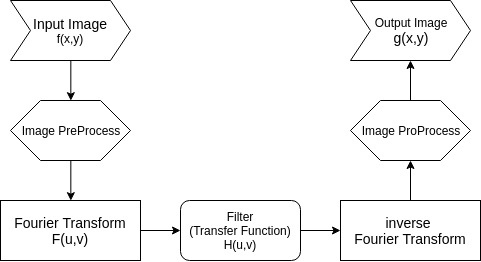
图像频率特性分析
频谱图上的每一个像素点都代表一个频率值,幅值由像素点亮度变码而得。对于一幅图像,图像信号的 频率特性 如下:
- 直流分量 表示预想的平均灰度
- 低频分量 代表了大面积背景区域和缓慢变化部分
- 高频分量 代表了它的边缘、细节、跳跃部分以及颗粒噪声
- 振幅 描述了图像灰度的亮度
- 相位 决定了图像是什么样子
数字图像的二维离散傅立叶变换所得的结果的频域成分如下图所示,左上角是直流成分,变换结果四个角周围对应于低频成分,中央部分对应于高频部分
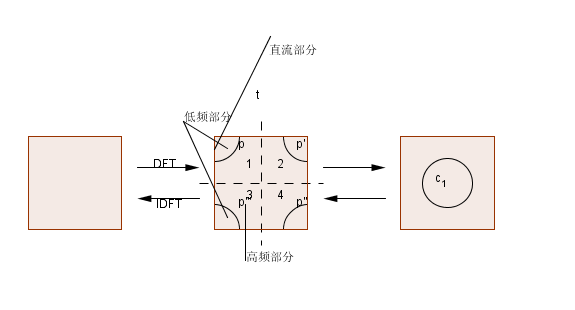
为了便于观察,常常采取 换位 方法使直流成分出现在窗口的中央(中心化),变换后中心为低频,向外是高频。
在频域,可以很方便的实现 图像的锐化和模糊:
- 截取频率的低频分量,对其作傅立叶反变换,得到的就是模糊后的图像,即 低通滤波
- 截取频率的高频分量,对其作傅立叶反变换,得到的就是锐化后的图像,即 高通滤波
图像滤波实践
下面,我们以 lena.bmp(点此下载) 图像进行滤波实践。
Python分析
(1)加载图像,并转换为 灰度图 为
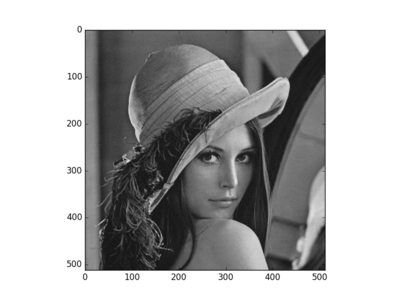
(2)对其 快速傅里叶变换,并经过 中心变换,得到 频率谱 和 相位谱

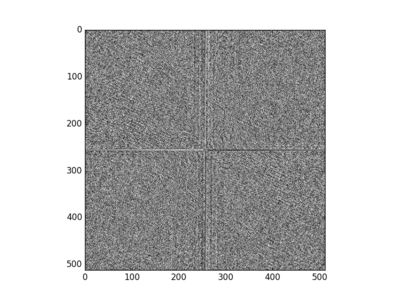
(3)分别截取 频谱图 的 低频部分(中间部分) 和 高频分量(四周部分)
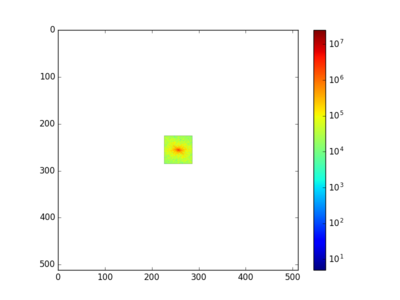

(4)对以上处理过的频谱图分别进行 反中心化、傅里叶反变换、取实部,得到 低通滤波 和 高通滤波 后的图像

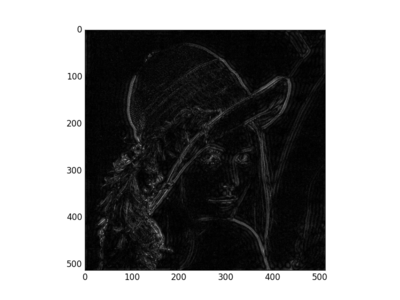
C++分析
使用 CImg 和 FFTW库 对 lena图像进行傅里叶变换(源代码见文末),结果如下

源代码
以上所有代码均存储在我的Github仓库:
- Python Code: cggos/cgocv_app/cv_py
- C++ Code: cggos/cgocv_app/image_process/fftw_demos
参考资料
智能推荐
python中文显示不出来_解决Python词云库wordcloud不显示中文的问题-程序员宅基地
文章浏览阅读2.6k次。解决Python词云库wordcloud不显示中文的问题2018-11-25背景:wordcloud是基于Python开发的词云生成库,功能强大使用简单。github地址:https://github.com/amueller/word_cloudwordcloud默认是不支持显示中文的,中文会被显示成方框。安装:安装命令:pip install wordcloud解决:经过测试发现不支持显示中文..._词云python代码无法输出文字
JVM在线分析-解决问题的工具一(jinfo,jmap,jstack)_jmap 在线分析-程序员宅基地
文章浏览阅读807次。扩展。_jmap 在线分析
台式计算机cpu允许温度,玩游戏cpu温度多少正常(台式电脑夏季CPU一般温度多少)...-程序员宅基地
文章浏览阅读1.1w次。随着炎热夏季的到来,当玩游戏正爽的时候,电脑突然死机了,自动关机了,是不是有想给主机一脚的冲动呢?这个很大的原因是因为CPU温度过高导致的。很多新手玩家可能都有一个疑虑,cpu温度多少以下正常?有些说是60,有些说是70,到底多高CPU温度不会死机呢?首先我们先看看如何查看CPU的温度。下载鲁大师并安装,运行鲁大师软件,即可进入软件界面,并点击温度管理,即可看到电脑各个硬件的温度。鲁大师一般情况下..._台式机玩游戏温度多少正常
小白自学Python日记 Day2-打印打印打印!_puthon打印任务收获-程序员宅基地
文章浏览阅读243次。Day2-打印打印打印!我终于更新了!(哭腔)一、 最简单的打印最最简单的打印语句: print(“打印内容”)注意:python是全英的,符号记得是半角下面是我写的例子:然后进入power shell ,注意:你需要使用cd来进入你保存的例子的文件夹,保存时名字应该取为xxx.py我终于知道为什么文件夹取名都建议取英文了,因为进入的时候是真的很麻烦!如果你没有进入正确的文件夹..._puthon打印任务收获
Docker安装:Errors during downloading metadata for repository ‘appstream‘:_"cenerrors during download metadata for repository-程序员宅基地
文章浏览阅读1k次。centos8问题参考CentOS 8 EOL如何切换源? - 云服务器 ECS - 阿里云_"cenerrors during download metadata for repository \"appstream"
尚硅谷_谷粒学苑-微服务+全栈在线教育实战项目之旅_基于微服务的在线教育平台尚硅谷-程序员宅基地
文章浏览阅读2.7k次,点赞3次,收藏11次。SpringBoot+Maven+MabatisPlusmaven在新建springboot项目引入RELEASE版本出错maven在新建springboot项目引入RELEASE版本出错maven详解maven就是通过pom.xml中的配置,就能够从仓库获取到想要的jar包。仓库分为:本地仓库、第三方仓库(私服)、中央仓库springframework.boot:spring-boot-starter-parent:2.2.1.RELEASE’ not found若出现jar包下载不了只有两_基于微服务的在线教育平台尚硅谷
随便推点
网络学习第六天(路由器、VLAN)_路由和vlan-程序员宅基地
文章浏览阅读316次。路由的概念路由器它称之为网关设备。路由器就是用于连接不同网络的设备路由器是位于OSI模型的第三层。路由器通过路由决定数据的转发。网关的背景:当时每家计算机厂商,用于交换数据的通信程序(协议)和数据描述格式各不相同。因此,就把用于相互转换这些协议和格式的计算机称为网关。路由器与三层交换器的对比路由协议对比路由器的作用:1.路由寻址2.实现不同网络之间相连的功能3.通过路由决定数据的转发,转发策略称为 路由选择。VLAN相关技术什么是VLAN?中文名称叫:虚拟局域网。虚_路由和vlan
设置div背景颜色透明度,内部元素不透明_div设置透明度,里面的内容不透明-程序员宅基地
文章浏览阅读2.8w次,点赞6次,收藏22次。设置div背景颜色透明度,内部元素不透明:.demo{ background-color:rgba(255,255,255,0.15) } 错误方式:.demo{ background-color:#5CACEE;opacity:0.75;} 这样会导致div里面的元素内容和背景颜色一起变透明只针对谷歌浏览器的测试_div设置透明度,里面的内容不透明
Discuz!代码大全-程序员宅基地
文章浏览阅读563次。1.[ u]文字:在文字的位置可以任意加入您需要的字符,显示为下划线效果。2.[ align=center]文字:在文字的位置可以任意加入您需要的字符,center位置center表示居中,left表示居左,right表示居右。5.[ color=red]文字:输入您的颜色代码,在标签的中间插入文字可以实现文字颜色改变。6.[ SIZE=数字]文字:输入您的字体大小,在标签的中间插入文..._discuzcode 大全
iOS NSTimer定时器-程序员宅基地
文章浏览阅读2.6k次。iOS中定时器有三种,分别是NSTimer、CADisplayLink、dispatch_source,下面就分别对这三种计时器进行说明。一、NSTimerNSTimer这种定时器用的比较多,但是特别需要注意释放问题,如果处理不好很容易引起循环引用问题,造成内存泄漏。1.1 NSTimer的创建NSTimer有两种创建方法。方法一:这种方法虽然创建了NSTimer,但是定时器却没有起作用。这种方式创建的NSTimer,需要加入到NSRunLoop中,有NSRunLoop的驱动才会让定时器跑起来。_ios nstimer
Linux常用命令_ls-lmore-程序员宅基地
文章浏览阅读4.8k次,点赞17次,收藏51次。Linux的命令有几百个,对程序员来说,常用的并不多,考虑各位是初学者,先学习本章节前15个命令就可以了,其它的命令以后用到的时候再学习。1、开机 物理机服务器,按下电源开关,就像windows开机一样。 在VMware中点击“开启此虚拟机”。2、登录 启动完成后,输入用户名和密码,一般情况下,不要用root用户..._ls-lmore
MySQL基础命令_mysql -u user-程序员宅基地
文章浏览阅读4.1k次。1.登录MYSQL系统命令打开DOS命令框shengfen,以管理员的身份运行命令1:mysql -u usernae -p password命令2:mysql -u username -p password -h 需要连接的mysql主机名(localhost本地主机名)或是mysql的ip地址(默认为:127.0.0.1)-P 端口号(默认:3306端口)使用其中任意一个就OK,输入命令后DOS命令框得到mysql>就说明已经进入了mysql系统2. 查看mysql当中的._mysql -u user