Dr_can模型预测控制笔记与代码实现-程序员宅基地
最近在准备毕业设计,通过看Dr_can的视频来学习一些控制方法,视频链接https://www.bilibili.com/video/BV1cL411n7KV/?spm_id_from=333.788.recommend_more_video.0
https://www.bilibili.com/video/BV1cL411n7KV/?spm_id_from=333.788.recommend_more_video.0
由于实际需要,后续应该会更新模型预测控制在非线性领域的应用(自适应MPC,增益预定MPC,非线性MPC)
1.最优控制与代价函数
最优控制(optimal control)指的是在一定的约束情况下达到最优状态的系统表现,其中约束情况通常是实际环境所带来的限制,比如说如果你去控制方向盘的转向,方向盘的转动自身是有一个极限位置的,再比如说,对于一个卫星控制系统,三轴输出的力,力矩都有自己的极大值。
而如何去定义一个最优状态呢?首先引入一个比较直观的例子,汽车的转向变道问题:
正常来说,汽车转向变道应当追求乘客舒适度情况,如下图;
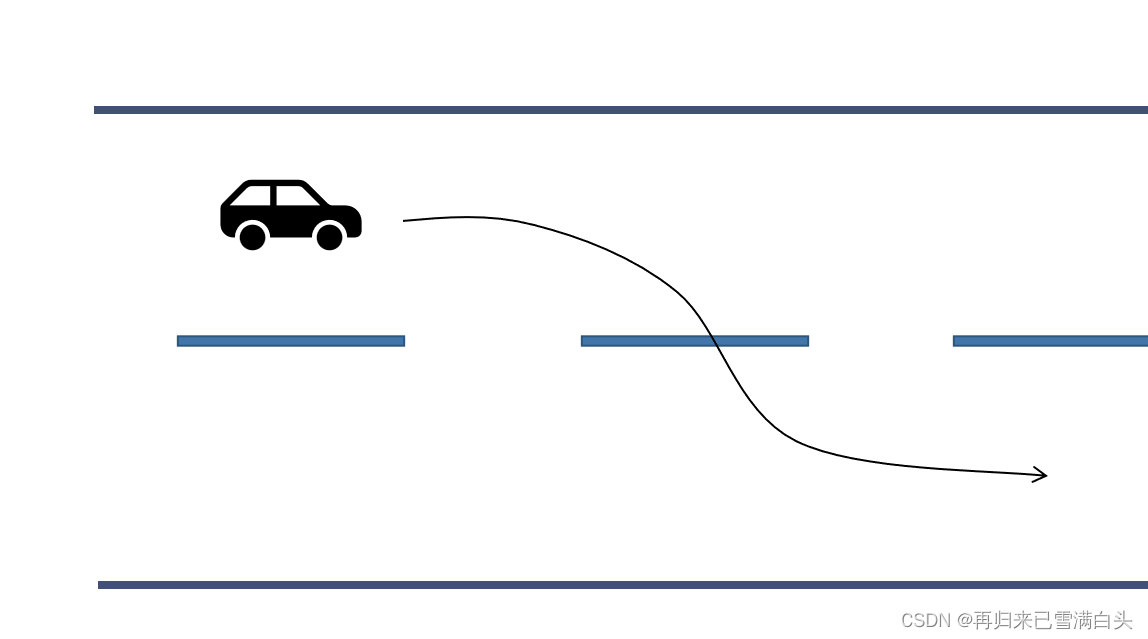
但如果考虑到紧急避障的问题,那么答案就完全不同了,如下图,当汽车前方遭遇到一辆校车急刹车时,为了躲开它,汽车必须尽快地向一侧变道,而不考虑舒适度问题。
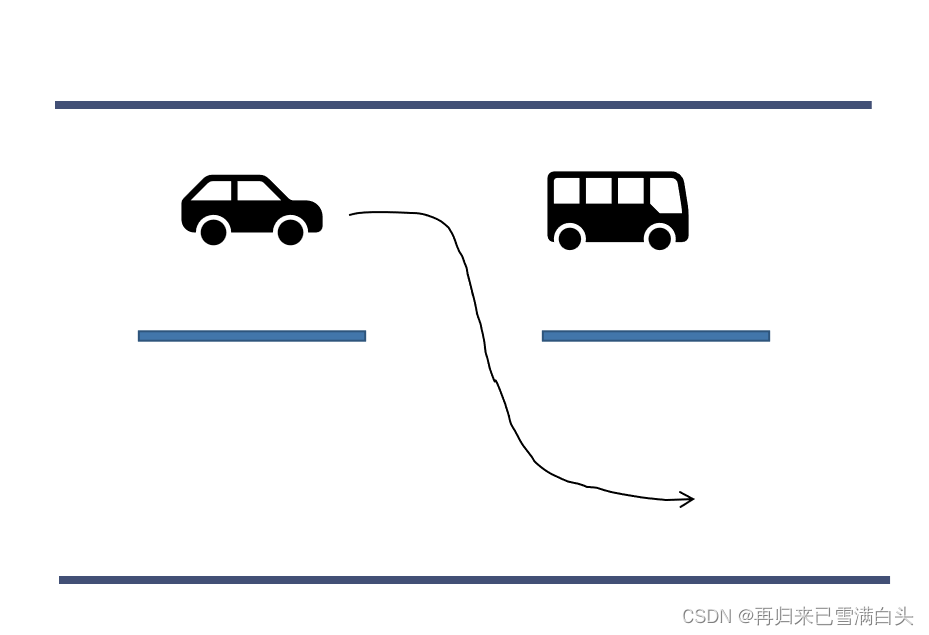
因此,最优是需要结合系统面临的实际情况得出的概念,对于不同的应用背景,应当设定不同的指标去衡量优劣,因此我们引入代价函数(Cost Function)的概念:
首先,对于单输入单输出系统(SISO)而言,衡量系统性能优劣可以用误差的积累值(越小,代表误差越小,收敛越快)和输入的积累值
(越小,代表控制耗能越少,越节约)来衡量。
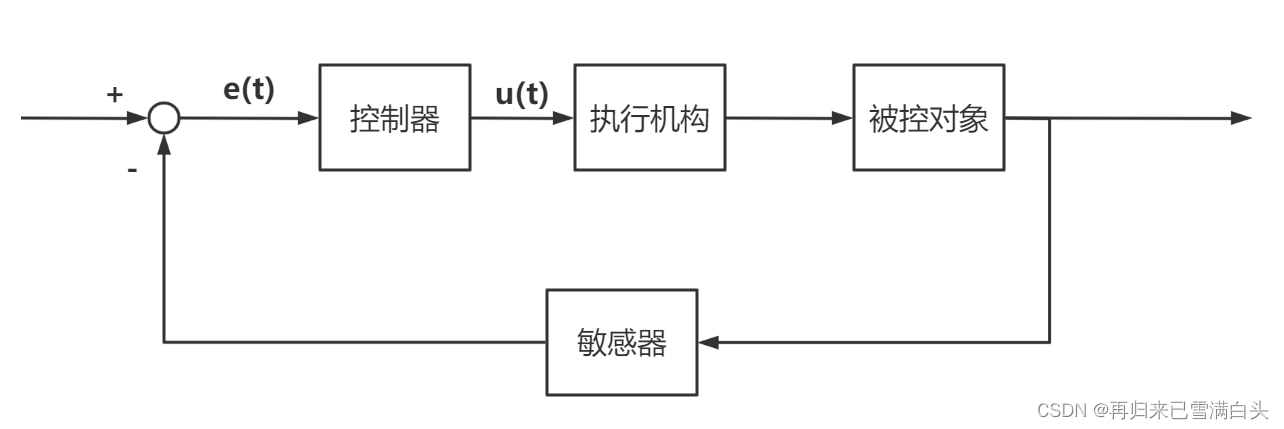
由此,我们可以定义代价函数:
函数中的q,r分别表示一个增益系数,如果q大,表示希望误差变得更小,收敛更快;r大,表示更注重输入累积,更注重节能。
接下来,我们把其推广到多输入多输出系统(MIMO),使用状态空间描述为:(这里我们假设前馈矩阵为0)
此时,衡量系统表现优劣就要引入二次型的知识,我们定义:
这里的Q和R矩阵一般是我们设定的对角矩阵,我们来举一个简单的例子:
我们假定期望输入是0,那么:
我们可以通过代价函数J的大小,来衡量系统表现的优劣,当代价函数取最小值时得到的输入,即可被称为是一种“最优输入”。
2.模型预测控制的引入
那么为什么还要引入模型预测控制的概念呢?最优控制中的代价函数需要计算从0时刻到正无穷时刻的积分,这是一种很贪婪的行为,需要消耗大量算力;同时,系统如果是一个时变系统,或者面临扰动的话,前一时刻得到的最优并不一定是下一时刻的最优值。
因而我们引入模型预测控制(Model Predictive Control)的概念,对于一般的离散化系统(因为实际计算机实现的控制系统都是离散的系统,连续系统离散化的方法在此不述)。在k时刻,我们可以测量或估计出系统的当前状态y(k),再通过计算得到的u(k),u(k+1),u(k+2)...u(k+j)得到系统未来状态的估计值y(k+1),y(k+2)...y(k+j);我们将预测估计的部分称为预测区间(Predictive Horizon),将控制估计的部分称为控制区间(Control Horizon),在得到最优输入之后,我们只施加当前时刻的输入u(k),而放弃接下来得到的输入序列。
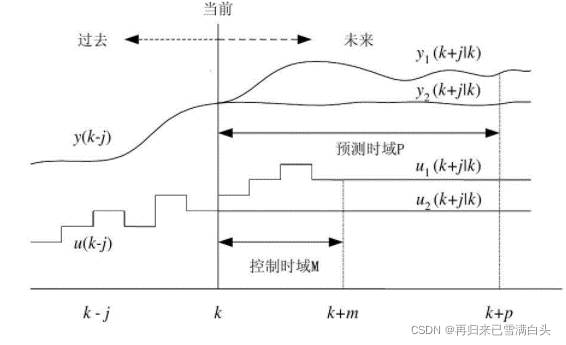
总结如下:模型预测控制在k时刻共需三步;
第一步:估计/测量读取系统的当前状态;
第二步:基于u(k),u(k+1),u(k+2)...u(k+j)进行最优化处理;
离散系统的代价函数可以参考
其中EN表示误差的终值,也是衡量优劣的一种标准。
第三步:只取u(k)作为控制输入施加在系统上。
在下一时刻重复以上三步,在下一步进行预测时使用的就是下一步的状态值,我们将这样的方案称为滚动优化控制(Receding Horizon Control)。
可以看到,每一时刻都需要进行一次预测,这对算力提出了巨大的要求,同时我们在此并没考虑约束问题,这个放在之后讨论。
3.最优化建模
实现MPC有许多方法,这里介绍一种方法:二次规划(Quadratic Programming)
我们首先引入一个离散系统:
我们定义:是k时刻预测的输入值,而
是k时刻预测的状态值,我们设:
对于期望输入为0,输出向量等于状态向量的离散系统:
我们可以得到代价函数:
其中,我们需要求解的是系统的输入u(k),这就需要我们把状态项x(k)给消除掉,处理这个事情需要利用系统的状态方程,首先有
我们可以通过传感器或者状态估计得到系统当前的状态值,这相当于系统的一个初值,由初值和状态方程可以得到其他项为:
我们把它简单整理一下,有:
我们再令:
我们就得到了最简单的形式:
即:
上式还可根据之前推导的公式继续化简,
其中,与
互为转置,但他们彼此又都是常数,所以他们彼此相等,因此有:
再令
有:
由此我们就得到了模型预测控制代价函数的简单形式。
4.一个详细建模实例与完整代码
下面直接上得到最优输入U_k的代码
function U_k=MPC(A,B,N,x_k,Q,R,F)
%%%%%%%%%%%%%%%%%%%%%%%%
n = size(A,1); %% A矩阵是n * n矩阵,得到A矩阵的维数
p = size(B,2); %% B矩阵是n * p矩阵,得到B矩阵的维数
M = [eye(n);zeros(N*n,n)]; %% 初始化M矩阵,第一个分块矩阵置单位阵,其余矩阵置零
C = zeros((N+1)*n,N*p); %% 初始化C矩阵,置零
%接下来计算完整的M矩阵与C矩阵
tmp = eye(n); %定义一个n阶单位阵,工具人
for i = 1:N
rows = i*n + (1:n);%行数,因为是分块矩阵所以从1至n;
C(rows, :) = [tmp*B, C(rows-n, 1:end-p)];%用遍历的方法将C矩阵填满;
tmp = A*tmp;%每次都左乘一次A矩阵;
M(rows,:) = tmp;%写满M矩阵;
end
%定义Q_bar和R_bar
S_q = size(Q,1);%得到Q矩阵维度
S_r = size(R,1);%得到R矩阵维度
Q_bar = zeros((N+1)*S_q,(N+1)*S_q);%定义Q_bar矩阵维度
R_bar = zeros(N*S_r,N*S_r);%定义R_bar矩阵维度
for i = 0:N-1
Q_bar(i*S_q+1:(i+1)*S_q,i*S_q+1:(i+1)*S_q) = Q;%把对角线上写满Q
end
Q_bar(N*S_q+1:(N+1)*S_q, N*S_q+1:(N+1)*S_q) = F;%最后一块写上F
for i = 0:N-1
R_bar(i*S_r+1:(i+1)*S_r, i*S_r+1:(i+1)*S_r) = R;%对角线上写满R
end
G = M'*Q_bar*M;%定义M矩阵,事实上在代价函数中,这和输入无关,并没有被用到
E = M'*Q_bar*C;%定义E矩阵
H = C'*Q_bar*C + R_bar;%定义H矩阵
%最优化,得到最优输入值
f = x_k'*E;%由于quadprog函数的定义,需要把其写成矩阵相乘形式
%基于实际情况,给输入加约束
D = eye(3);b = [10;10;10];Aep=[];Bep=[];c=[1;1;1];d=[-1;-1;-1];
U_k = quadprog(H,f,D,b,Aep,Bep,d,c);%求解最优的U_k值代码中有几个值得注意的点:
1.矩阵的维度,这里面涉及矩阵很多,很容易把维度搞晕,建议自己手推一次,效果很好。
2.这段填满C矩阵的过程稍微有点难懂,是对照着C矩阵的结构以及里面的规律写出来的。
for i = 1:N
rows = i*n + (1:n);%行数,因为是分块矩阵所以从1至n;
C(rows, :) = [tmp*B, C(rows-n, 1:end-p)];%用遍历的方法将C矩阵填满;
tmp = A*tmp;%每次都左乘一次A矩阵;
M(rows,:) = tmp;%写满M矩阵;
end3.得到最优控制输入的函数quadprog,根据Matlab自带文档描述,它是求解下列问题最小值的函数,可以添加约束,由一个二次型描述与一个线性描述组成,为了使控制器的表现更贴近实际,我给输出加了正负1的限制。
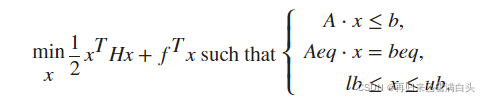
接下来,我来做一个完整的仿真过程,并比对不同Q,F,R对系统的影响,假设有离散系统为:
我们设A矩阵,B矩阵分别为:
输出的期望值为零向量,设置不同的Q,R,F矩阵,进行仿真;
在第一种情况,我们令:
在第二种情况,我们令:
显然,在第一种情况我们更在意误差的收敛速度,而在第二种情况我们更在意能量消耗的多少,下面是仿真结果:
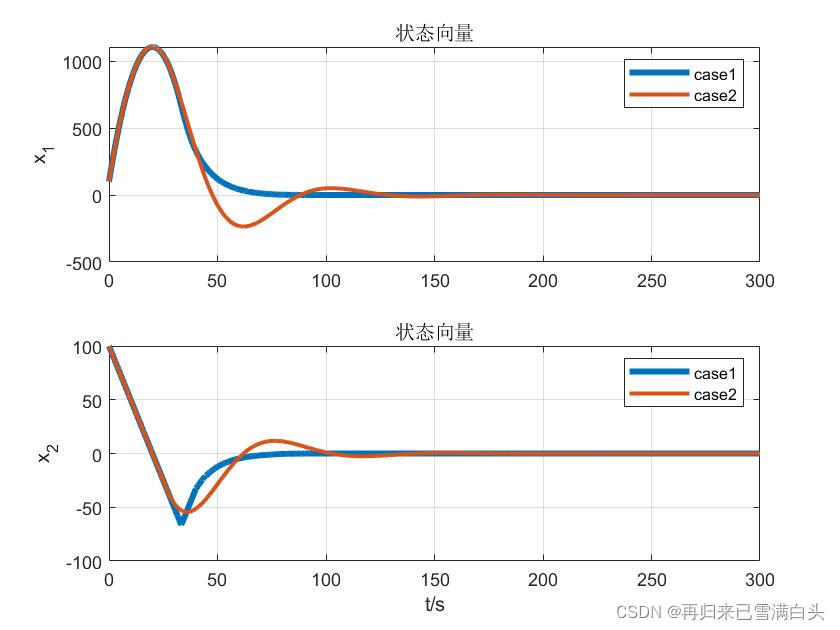
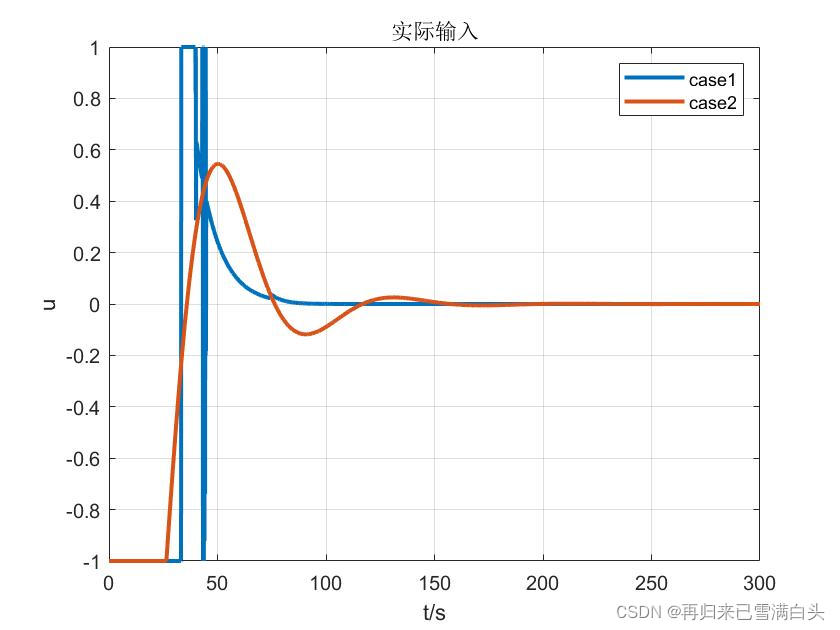

可以明显得看到,情况一收敛速度更快,耗能更多,而情况二收敛速度更慢,耗能更少,符合之前的预测。
下面是完整仿真代码:
%h为一个更新周期,即积分步长,采样时间为n
%假定输入为零,输出即为状态值
clear
clc
format long
%--------------------------初始参数---------------------------------%
h=0.1; %仿真步长
n=300; %仿真时间
NN=n/h;
A = [1,0.1;0,1]; %系统矩阵
B = [0;0.5]; %输入矩阵
Q = [2,0;0,2]; %Q矩阵,对误差积累的重视程度
R = 0.1; %R系数,表示对节省输入的重视程度
N = 3; %预测区间
F = [2,0;0,2]; %F矩阵,对终端误差的重视程度
x_0 = [100;100]; %初始位置
X1 = zeros(2,NN+1);
t = zeros(1,NN+1);
U1 = zeros(1,NN+1); %初始化
Eg1 = zeros(1,NN+1);
X1(:,1) = x_0; %赋初值
%--------------------------仿真1开始---------------------------------%
for j = 1:NN
U_all = MPC(A,B,N,X1(:,j),Q,R,F);
X1(:,j+1) = A*X1(:,j) + B*U_all(1); %这里只取预测估计的第一项
U1(j) = U_all(1);
t(j+1)=t(j)+h;
Eg1(j+1) = Eg1(j)+U_all(1)^2;
end
%%为了比较不同参数的影响,选择另一组Q,R,F
Q = [0.1,0;0,0.1]; %Q矩阵,对误差积累的重视程度
R = 10; %R系数,表示对节省输入的重视程度
F = [0.1,0;0,0.1]; %F矩阵,对终端误差的重视程度
X2 = zeros(2,NN+1);
U2 = zeros(1,NN+1); %初始化
Eg2 = zeros(1,NN+1);
X2(:,1) = x_0; %赋初值
%--------------------------仿真2开始---------------------------------%
for j = 1:NN
U_all = MPC(A,B,N,X2(:,j),Q,R,F);
X2(:,j+1) = A*X2(:,j) + B*U_all(1); %这里只取预测估计的第一项
U2(j) = U_all(1);
t(j+1)=t(j)+h;
Eg2(j+1) = Eg2(j)+U_all(1)^2;
end
figure(1)
subplot(2,1,1),plot(t,X1(1,:),'-','linewidth',3),title('状态向量'),ylabel('x_1');hold on;
plot(t,X2(1,:),'-','linewidth',2),title('状态向量'),ylabel('x_1');grid on;
legend('case1','case2');
subplot(2,1,2),plot(t,X1(2,:),'-','linewidth',3),xlabel('t/s'),ylabel('x_2');hold on
plot(t,X2(2,:),'-','linewidth',2),title('状态向量'),ylabel('x_2');grid on;
legend('case1','case2');
figure(2)
plot(t,U1,'linewidth',2),title('实际输入'),xlabel('t/s'),ylabel('u');hold on;
plot(t,U2,'linewidth',2),title('实际输入'),xlabel('t/s'),ylabel('u');grid on;
legend('case1','case2');
figure(3)
plot(t,Eg1,'linewidth',2),title('消耗能量'),xlabel('t/s'),ylabel('J');hold on;
plot(t,Eg2,'linewidth',2),title('消耗能量'),xlabel('t/s'),ylabel('J');grid on;
legend('case1','case2');智能推荐
解决win10/win8/8.1 64位操作系统MT65xx preloader线刷驱动无法安装_mt65驱动-程序员宅基地
文章浏览阅读1.3w次。转载自 http://www.miui.com/thread-2003672-1-1.html 当手机在刷错包或者误修改删除系统文件后会出现无法开机或者是移动定制(联通合约机)版想刷标准版,这时就会用到线刷,首先就是安装线刷驱动。 在XP和win7上线刷是比较方便的,用那个驱动自动安装版,直接就可以安装好,完成线刷。不过现在也有好多机友换成了win8/8.1系统,再使用这个_mt65驱动
SonarQube简介及客户端集成_sonar的客户端区别-程序员宅基地
文章浏览阅读1k次。SonarQube是一个代码质量管理平台,可以扫描监测代码并给出质量评价及修改建议,通过插件机制支持25+中开发语言,可以很容易与gradle\maven\jenkins等工具进行集成,是非常流行的代码质量管控平台。通CheckStyle、findbugs等工具定位不同,SonarQube定位于平台,有完善的管理机制及强大的管理页面,并通过插件支持checkstyle及findbugs等既有的流..._sonar的客户端区别
元学习系列(六):神经图灵机详细分析_神经图灵机方法改进-程序员宅基地
文章浏览阅读3.4k次,点赞2次,收藏27次。神经图灵机是LSTM、GRU的改进版本,本质上依然包含一个外部记忆结构、可对记忆进行读写操作,主要针对读写操作进行了改进,或者说提出了一种新的读写操作思路。神经图灵机之所以叫这个名字是因为它通过深度学习模型模拟了图灵机,但是我觉得如果先去介绍图灵机的概念,就会搞得很混乱,所以这里主要从神经图灵机改进了LSTM的哪些方面入手进行讲解,同时,由于模型的结构比较复杂,为了让思路更清晰,这次也会分开几..._神经图灵机方法改进
【机器学习】机器学习模型迭代方法(Python)-程序员宅基地
文章浏览阅读2.8k次。一、模型迭代方法机器学习模型在实际应用的场景,通常要根据新增的数据下进行模型的迭代,常见的模型迭代方法有以下几种:1、全量数据重新训练一个模型,直接合并历史训练数据与新增的数据,模型直接离线学习全量数据,学习得到一个全新的模型。优缺点:这也是实际最为常见的模型迭代方式,通常模型效果也是最好的,但这样模型迭代比较耗时,资源耗费比较多,实时性较差,特别是在大数据场景更为困难;2、模型融合的方法,将旧模..._模型迭代
base64图片打成Zip包上传,以及服务端解压的简单实现_base64可以装换zip吗-程序员宅基地
文章浏览阅读2.3k次。1、前言上传图片一般采用异步上传的方式,但是异步上传带来不好的地方,就如果图片有改变或者删除,图片服务器端就会造成浪费。所以有时候就会和参数同步提交。笔者喜欢base64图片一起上传,但是图片过多时就会出现数据丢失等异常。因为tomcat的post请求默认是2M的长度限制。2、解决办法有两种:① 修改tomcat的servel.xml的配置文件,设置 maxPostSize=..._base64可以装换zip吗
Opencv自然场景文本识别系统(源码&教程)_opencv自然场景实时识别文字-程序员宅基地
文章浏览阅读1k次,点赞17次,收藏22次。Opencv自然场景文本识别系统(源码&教程)_opencv自然场景实时识别文字
随便推点
ESXi 快速复制虚拟机脚本_exsi6.7快速克隆centos-程序员宅基地
文章浏览阅读1.3k次。拷贝虚拟机文件时间比较长,因为虚拟机 flat 文件很大,所以要等。脚本完成后,以复制虚拟机文件夹。将以下脚本内容写入文件。_exsi6.7快速克隆centos
好友推荐—基于关系的java和spark代码实现_本关任务:使用 spark core 知识完成 " 好友推荐 " 的程序。-程序员宅基地
文章浏览阅读2k次。本文主要实现基于二度好友的推荐。数学公式参考于:http://blog.csdn.net/qq_14950717/article/details/52197565测试数据为自己随手画的关系图把图片整理成文本信息如下:a b c d e f yb c a f gc a b dd c a e h q re f h d af e a b gg h f bh e g i di j m n ..._本关任务:使用 spark core 知识完成 " 好友推荐 " 的程序。
南京大学-高级程序设计复习总结_南京大学高级程序设计-程序员宅基地
文章浏览阅读367次。南京大学高级程序设计期末复习总结,c++面向对象编程_南京大学高级程序设计
4.朴素贝叶斯分类器实现-matlab_朴素贝叶斯 matlab训练和测试输出-程序员宅基地
文章浏览阅读3.1k次,点赞2次,收藏12次。实现朴素贝叶斯分类器,并且根据李航《统计机器学习》第四章提供的数据训练与测试,结果与书中一致分别实现了朴素贝叶斯以及带有laplace平滑的朴素贝叶斯%书中例题实现朴素贝叶斯%特征1的取值集合A1=[1;2;3];%特征2的取值集合A2=[4;5;6];%S M LAValues={A1;A2};%Y的取值集合YValue=[-1;1];%数据集和T=[ 1,4,-1;..._朴素贝叶斯 matlab训练和测试输出
Markdown 文本换行_markdowntext 换行-程序员宅基地
文章浏览阅读1.6k次。Markdown 文本换行_markdowntext 换行
错误:0xC0000022 在运行 Microsoft Windows 非核心版本的计算机上,运行”slui.exe 0x2a 0xC0000022″以显示错误文本_错误: 0xc0000022 在运行 microsoft windows 非核心版本的计算机上,运行-程序员宅基地
文章浏览阅读6.7w次,点赞2次,收藏37次。win10 2016长期服务版激活错误解决方法:打开“注册表编辑器”;(Windows + R然后输入Regedit)修改SkipRearm的值为1:(在HKEY_LOCAL_MACHINE–》SOFTWARE–》Microsoft–》Windows NT–》CurrentVersion–》SoftwareProtectionPlatform里面,将SkipRearm的值修改为1)重..._错误: 0xc0000022 在运行 microsoft windows 非核心版本的计算机上,运行“slui.ex